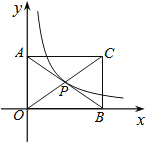单选题
下列各点不在反比例函数y= 的图象上的应是( )
的图象上的应是( )
- A、 (6,-2)
- B、 (6,2)
- C、 (3,4)
- D、 (-3,-4)
如果反比例函数 的图像经过点(-1,2),那么这个反比例函数的图象一定经过点( )
的图像经过点(-1,2),那么这个反比例函数的图象一定经过点( )
- A、 (
, 2);
- B、 (
, 2);
- C、 (2,-1);
- D、 (-2,-1).
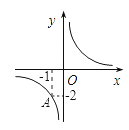
如图,反比例函数的图象经过点A(-1,-2).则当x>1时,函数值y的取值范围是( )
- A、 y>1
- B、 0<y<1
- C、 y>2
- D、 0< y<2
如果反比例函数y= 的图象经过点(-1,-2),则k的值是( )
的图象经过点(-1,-2),则k的值是( )
- A、 2
- B、 -2
- C、 -3
- D、 3
如图,双曲线y=的一个分支为( )
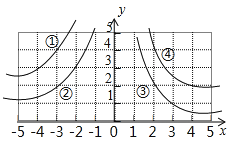
- A、 ①
- B、 ②
- C、 ③
- D、 ④
已知反比例函数的图象经过点(-1,2),则它的解析式是( )
- A、
- B、
- C、
- D、
如图是我们学过的反比例函数图象,它的函数解析式可能是( )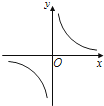
- A、
- B、
- C、
- D、 y=
已知点P(-1,3)在反比例函数 的图象上,则k的值是 ( )
的图象上,则k的值是 ( )
- A、
- B、
- C、 3
- D、 -3
下列图象中是反比例函数  图象的是( )
图象的是( )
- A、
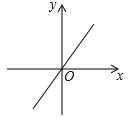
- B、
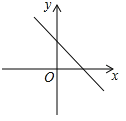
- C、
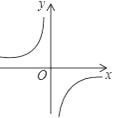
- D、
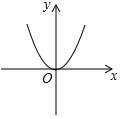
某反比例函数象经过点(-1,6),则下列各点中此函数图象也经过的是( )
- A、 (-3,2)
- B、 (3,2)
- C、 (2,3)
- D、 (6,1)
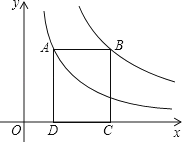
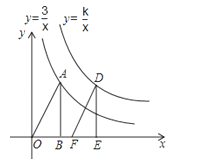
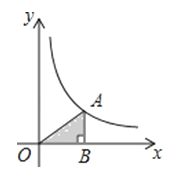
如图,在平面直角坐标系中,点A是双曲线y=(x>0)上的一个动点,过点A作x轴的垂线,交x轴于点B,点A运动过程中△AOB的面积将会( )
- A、 逐渐增大
- B、 逐渐减小
- C、 先增大后减小
- D、 不变
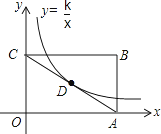
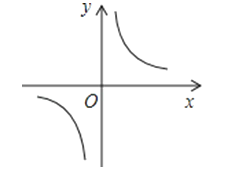
已知反比例函数y=的图象如图所示,则实数m的取值范围是( )
- A、 m>1
- B、 m>0
- C、 m<1
- D、 m<0
若点A(﹣5,y1),B(﹣3,y2),C(2,y3)在反比例函数y=  的图象上,则y1 , y2 , y3的大小关系是( )
的图象上,则y1 , y2 , y3的大小关系是( )
- A、 y1<y3<y2
- B、 y1<y2<y3
- C、 y3<y2<y1
- D、 y2<y1<y3