2017高考数学备考复习（文科）专题十二：统计案例-组卷题库站

单选题

对变量 $\text{[math]}$ 与 $\text{[math]}$ ，分别选择了4个不同的回归方程甲、乙、丙、丁，它们的相关系数 $\text{[math]}$ 分别为： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ . 其中拟合效果最好的是方程（）.

A、甲

B、乙

C、丙

D、丁

工人月工资y（元）与劳动生产率x（千元）变化的回归方程 $\text{[math]}$ ，下列判断正确的是 ( )　
①劳动生产率为1千元时，工资约为130元　
②劳动生产率提高1千元时，月工资约提高80元　
③劳动生产率提高1千元时，月工资约提高130元　
④当月工资为210元时，劳动生产率约为2千元　

A、 ① ②　

B、 ① ② ④　

C、 ② ④　

D、 ① ② ③ ④

已知变量 $\text{[math]}$ 和 $\text{[math]}$ 满足关系 $\text{[math]}$ ，变量 $\text{[math]}$ 与 $\text{[math]}$ 正相关. 下列结论中正确的是（）

A、 $\text{[math]}$ 与 $\text{[math]}$ 负相关， $\text{[math]}$ 与 $\text{[math]}$ 负相关

B、 $\text{[math]}$ 与 $\text{[math]}$ 正相关， $\text{[math]}$ 与 $\text{[math]}$ 正相关

C、 $\text{[math]}$ 与 $\text{[math]}$ 正相关， $\text{[math]}$ 与 $\text{[math]}$ 负相关

D、 $\text{[math]}$ 与 $\text{[math]}$ 负相关， $\text{[math]}$ 与 $\text{[math]}$ 正相关

下表是一位母亲给儿子作的成长记录：

年龄/周岁	3	4	5	6	7	8	9
身高/cm	94.8	104.2	108.7	117.8	124.3	130.8	139.1

根据以上样本数据，她建立了身高 y （cm）与年龄x（周岁）的线性回归方程为 $\text{[math]}$ =7.19x+73.93，给出下列结论：

①y与x具有正的线性相关关系；

②回归直线过样本的中心点（42，117.1）；

③儿子10岁时的身高是145.83 cm；

④儿子年龄增加1周岁，身高约增加 7.19 cm.

其中，正确结论的个数是（）

A、 1

B、 2

C、 3

D、 4

某高校《统计》课程的教师随机给出了选该课程的一些情况，具体数据如下：

	非统计专业	统计专业
男	13	10
女	7	20

为了判断选修统计专业是否与性别有关，根据表中数据，得，因为，所以可以判定选修统计专业与性别有关.那么这种判断出错的可能性为（）

A、 5%

B、 95%

C、 1%

D、 99%

A、 t₁和t₂有交点（s，t）

B、 t₁和t₂相交，但交点不是（s，t）

C、 t₁和t₂必定重合

D、 t₁和t₂必定不重合

如图所示，样本A和B分别取自两个不同的总体，它们的样本平均数分别为 $\text{[math]}$ 、 $\text{[math]}$ ，样本标准差分别为S_A ， S_B ，则（）

A、 $\text{[math]}$ ＞ $\text{[math]}$ ，S_A＞S_B

B、 $\text{[math]}$ ＜ $\text{[math]}$ ，S_A＞S_B

C、 $\text{[math]}$ ＞ $\text{[math]}$ ，S_A＜S_B

D、 $\text{[math]}$ ＜ $\text{[math]}$ ，S_A＜S_B

已知具有线性相关关系的两个变量x，y之间的一组数据如表：

x	0	1	2	3	4
y	2.2	4.3	4.5	4.8	6.7

且回归直线方程为 $\text{[math]}$ =bx+2.6，根据模型预报当x=6时，y的预测值为（）

A、 5.76

B、 6.8

C、 8.3

D、 8.46

有线性相关关系的两个变量x与y有如表对应关系，则其线性回归直线必过点（）

x	2	3	4	5	6
y	2.2	3.8	5.5	6.5	7.0

A、（4，5.5）

B、（4，5）

C、（5，5）

D、（6，7）

有一位同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经过统计得到了一天所卖的热饮杯数（y）与当天气温（x℃）之间的线性关系，其回归方程为 $\text{[math]}$ =﹣2.35x+147.77．如果某天气温为2℃时，则该小卖部大约能卖出热饮的杯数是（）

A、 140

B、 143

C、 152

D、 156

通过随机询问11名性别不同的大学生是否爱好某项运动，得到如下的列联表：

	男	女	总计
爱好	40	20	60
不爱好	20	30	50
总计	60	50	110

参照附表，得到的正确结论是（）

A、有99%以上的把握认为“爱好该项运动与性别有关”

B、有99%以上的把握认为“爱好该项运动与性别无关”

C、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”

D、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”

某商场为了了解毛衣的月销售量y（件）与月平均气温x（℃）之间的关系，随机统计了某4个月的月销售量与当月平均气温，其数据如下表：

月平均气温x（℃）	17	13	8	2
月销售量y（件）	24	33	40	55

由表中数据算出线性回归方程 $\text{[math]}$ =bx+a中的b=﹣2，气象部门预测下个月的平均气温约为6℃，据此估计该商场下个月毛衣销售量约为（）件．

A、 46

B、 40

C、 38

D、 58

在2013年9月15日，某市物价部门对本市的5家商场的某种商品的一天销售量及其价格进行调查，5家商场的售价x元和销售量y件之间的一组数据如下表所示：

价格x	9	9.5	10	10.5	11
销售量y	11	10	8	6	5

由散点图可知，销售量y与价格x之间有较好的线性相关关系，其线性回归方程是：y=﹣3.2x+a，则a=（）

A、 ﹣24

B、 35.6

C、 40.5

D、 40

通过随机询问110名性别不同的大学生是否爱好某项运动，得到如下的列联表：

	男	女	合计
爱好	40	20	60
不爱好	20	30	50
合计	60	50	110

根据上述数据能得出的结论是（）

（参考公式与数据：X²= $\text{[math]}$ ．当X²＞3.841时，有95%的把握说事件A与B有关；当X²＞6.635时，有99%的把握说事件A与B有关；当X²＜3.841时认为事件A与B无关．）

A、有99%的把握认为“爱好该项运动与性别有关”

B、有99%的把握认为“爱好该项运动与性别无关”

C、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别有关”

D、在犯错误的概率不超过0.1%的前提下，认为“爱好该项运动与性别无关”．

下列四个图各反映了两个变量的某种关系，其中可以看作具有较强线性相关关系的是（）

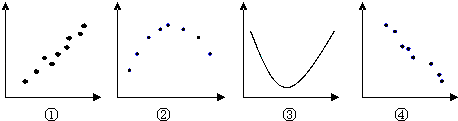
A、 ①③

B、 ①④

C、 ②③

D、 ①②

填空题

为考察高中生的性别与是否喜欢数学课程之间的关系，在我市某普通中学高中生中随机抽取200名学生，得到如下2×2列联表：

	喜欢数学课	不喜欢数学课	合计
男	30	60	90
女	20	90	110
合计	50	150	200

经计算K²≈6.06，根据独立性检验的基本思想，约有（填百分数）的把握认为“性别与喜欢数学课之间有关系”.

为了调查患慢性气管炎是否与吸烟有关，调查了339名50岁以上的人，调查结果如下表

	患慢性气管炎	未患慢性气管炎	合计
吸烟	43	162	205
不吸烟	13	121	134
合计	56	283	339

根据列联表数据，求得K² = .

某同学在求解某回归方程中，已知x，y的取值结果（y与x呈线性相关）如表：

x	2	3	4
y	6	4	m

并且求得了线性回归方程为 $\text{[math]}$ =﹣ $\text{[math]}$ x+ $\text{[math]}$ ，则m等于．

某地区2007年至2013年农村居民家庭人均纯收入y（单位：千元）的统计数据如表，

年份	2007	2008	2009	2010	2011	2012	2013
年份代号x	1	2	3	4	5	6	7
y	2.9	3.3	3.6	4.4	4.8	5.2	5.9

据此，我们得到y关于年份代号x的线性回归方程： $\text{[math]}$ =0.5 $\text{[math]}$ +2.3，则预测该地区2015年农村居民家庭人均纯收入等于．

已知x、y的取值如表所示：

x	0	1	3	4
y	2.2	4.3	4.8	6.7

从散点图分析，y与x线性相关，且 $\text{[math]}$ =0.95x+a，则a=．

综合题

某种产品的广告费用支出x万元与销售额y万元之间有如下的对应数据：

x	2	4	5	6	8
y	30	40	60	50	70

某种产品的广告费支出x与销售额y（单位：万元）之间有如下对应数据：

x	2	4	5	6	8
y	30	40	60	50	70

某种产品的广告费支出x与销售额y（单位：百万元）之间有如下对应：

X	2	4	5	6	8
y	30	40	60	50	70

“女大学生就业难”究竟有多难？其难在何处？女生在求职中是否收到了不公平对待？通过对某大学应届毕业生的调查与实证分析试对下列问题提出解答．为调查某地区大学应届毕业生的调查，用简单随机抽样方法从该地区抽取了500为大学生做问卷调查，结果如下：

性别

是否公平

男

女

公平

不公平

160

270

某成衣批发店为了对一款成衣进行合理定价，将该款成衣按事先拟定的价格进行试销，得到了如下数据：

批发单价x（元）	80	82	84	86	88	90
销售量y（件）	90	84	83	80	75	68

2017高考数学备考复习（文科）专题十二：统计案例

单选题

填空题

综合题

相关试卷推荐

友情链接