选择题
若反比例函数y=﹣ 
的图象经过点A（3，m），则m的值是（ ）
- A、 ﹣3
- B、 3
- C、 ﹣
- D、
下列图形既是轴对称图形又是中心对称图形的是（ ）
- A、
- B、
- C、
- D、
下列事件中，必然发生的是（ ）
- A、 某射击运动射击一次，命中靶心
- B、 通常情况下，水加热到100℃时沸腾
- C、 掷一次骰子，向上的一面是6点
- D、 抛一枚硬币，落地后正面朝上
如图，直线y=kx与双曲线y=﹣ 
交于A（x1 ， y1），B（x2 ， y2）两点，则2x1y2﹣8x2y1的值为（ ）
- A、 ﹣6
- B、 ﹣12
- C、 6
- D、 12
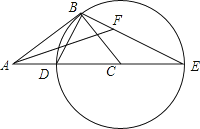
如上图，经过原点O的⊙P与 
、 
轴分别交于A、B两点，点C是劣弧 
上一点，则∠ACB=（ ）
- A、 80°
- B、 90°
- C、 100°
- D、 无法确定
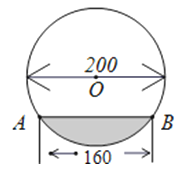
在直径为200cm的圆柱形油槽内装入一些油以后，截面如图．若油面的宽AB=160cm，则油的最大深度为（ ）
- A、 40cm
- B、 60cm
- C、 80cm
- D、 100cm
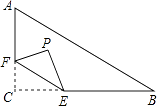
如图，在平面直角坐标系中，点B，C，E，在y轴上，Rt△ABC经过变换得到Rt△ODE．若点C的坐标为（0，1），AC=2，则这种变换可以是（ ）
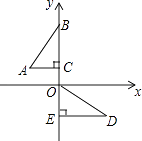
- A、 △ABC绕点C顺时针旋转90°，再向下平移3
- B、 △ABC绕点C顺时针旋转90°，再向下平移1
- C、 △ABC绕点C逆时针旋转90°，再向下平移1
- D、 △ABC绕点C逆时针旋转90°，再向下平移3
抛物线y=（m﹣1）x2﹣mx﹣m2+1的图象过原点，则m的值为（ ）
- A、 ±1
- B、 0
- C、 1
- D、 -1
圆的面积公式S=πR2中，S与R之间的关系是（ ）
- A、 S是R的正比例函数
- B、 S是R的一次函数
- C、 S是R的二次函数
- D、 以上答案都不对
如图，P是⊙O直径AB延长线上的一点，PC与⊙O相切于点C，若∠P=20°，则∠A的度数为（ ）
- A、 40°
- B、 35°
- C、 30°
- D、 25°
如图，一个大正方形中有2个小正方形，如果它们的面积分别是S1 ， S2 ， 则（ )
- A、 S2＞S1
- B、 S1=S2
- C、 S1＞S2
- D、 S1≥S2
