选择题:
下列现象是数学中的平移的是( )
- A、 树叶从树上落下
- B、 电梯从底楼升到顶楼
- C、 碟片在光驱中运行
- D、 卫星绕地球运动
∠1与∠2是内错角,∠1=30°,则∠2的度数为( )
- A、 30°
- B、 150°
- C、 30°或150°
- D、 不能确定
下列运算正确的是( )
- A、 a2•a3=a6
- B、 (﹣a2)3=﹣a6
- C、 (ab)2=ab2
- D、 a6÷a3=a2
已知三角形的两边长分别为5和7,则第三边长不可能是( )
- A、 1
- B、 3
- C、 5
- D、 7
若(x﹣1)0=1,则( )
- A、 x≥1
- B、 x≤1
- C、 x≠1
- D、 x≠0
如图,在△ABC中,∠C=50°,按图中虚线将∠C剪去后,∠1+∠2等于( )
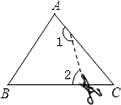
- A、 230°
- B、 210°
- C、 130°
- D、 310°
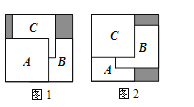
把三张大小相同的正方形卡片A、B、C叠放在一个底面为正方形的盒底上,底面未被卡片覆盖的部分用阴影表示,若按图1摆放时,阴影部分的面积为S1;若按图2摆放时,阴影部分的面积为S2 , 则S1与S2的大小关系是( )
- A、 S1>S2
- B、 S1<S2
- C、 S1=S2
- D、 无法确定