选择题:本题共12小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合题目要求的。
已知集合M=  ,N=
,N=  ,则M
,则M  N=( )
N=( )
- A、
- B、
- C、
- D、
设复数z满足  ,z在复平面内对应的点为(x,y),则( )
,z在复平面内对应的点为(x,y),则( )
- A、
- B、
- C、
- D、
已知a=log20.2,b=  ,c=
,c=  ,则( )
,则( )
- A、 a<b<c
- B、 a<c<b
- C、 c<a<b
- D、 b<c<a
古希腊吋期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是  ,称为黄金分割比例),著名的“断臂维纳斯“便是如此。此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度也是
,称为黄金分割比例),著名的“断臂维纳斯“便是如此。此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度也是  。若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是( )
。若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是( )

- A、 165cm
- B、 175cm
- C、 185cm
- D、 190cm
函数f(x)=  在[-
在[-  ,
,  ]。的图像大致为( )
]。的图像大致为( )
- A、

- B、
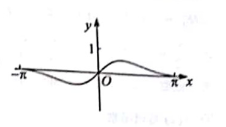
- C、
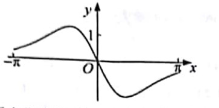
- D、
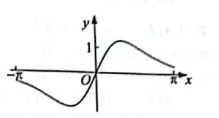
我国古代典籍《周易》用“卦”描述万物的变化。每一“重卦”由从下到上排列的6个爻组成,爻分为阳爻“——”和阴爻“--",下图就是一重卦。在所有重卦中随机取一重卦,则该重卦恰有3个阳爻的概率是( )

- A、
- B、
- C、
- D、
已知非零向量  ,
,  满足|
满足|  |=2|
|=2|  |,且
|,且  ,则
,则  与
与  的夹角为( )
的夹角为( )
- A、
- B、
- C、
- D、
下图是求  的程序框图,图中空白框中应填入( )
的程序框图,图中空白框中应填入( )

- A、 A=
- B、 A=2+
- C、 A=
- D、 A=1+
记Sn为等差数列  的前n项和。已知
的前n项和。已知  =0,
=0,  =5,则( )
=5,则( )
- A、 an=2n-5
- B、 an=3n-10
- C、 Sn=2n2-8n
- D、 Sn=
n2-2n
已知椭圆C的焦点为F1(-1,0),F2(1,0)。过F2的直线与C交于A,B两点。若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为( )
- A、
+y2=1
- B、
+
=1
- C、
+
=1
- D、
+
=1