江苏省连云港市灌云县西片2019-2020学年八年级上学期数学10月月考试卷

日期: 2025-03-30 月考试卷来源：出卷网

单选题

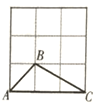
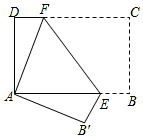
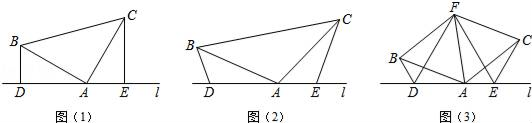
下列图形中是轴对称的是（）

A、

B、

C、

D、

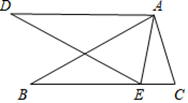
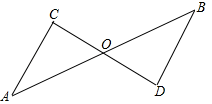
如图，△ABO≌△DCO，∠D=80°，∠DOC=70°，则∠B=（）.

A、 35°

B、 30°

C、 25°

D、 20°

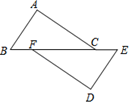
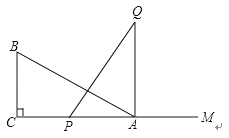
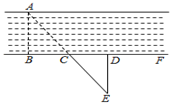
如图，要测量河两岸相对的两点A，B的距离，先在AB的垂线BF上取两点C、D，使CD＝BC，再作出BF的垂线DE，使A，C，E在一条直线上，可以说明△EDC≌△ABC最恰当的理由是（）

A、边角边

B、角边角

C、边边边

D、边边角

如图，在 $\text{[math]}$ 正方形网格中，已将图中的四个小正方形涂上阴影，若再从图中选一个涂上阴影，使得整个阴影部分组成的图形是轴对称图形，那么不符合条件的小正方形是（）

A、 ①

B、 ②

C、 ③

D、 ④

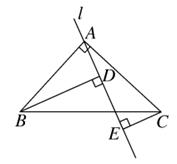
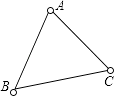
如图，兔子的三个洞口A、B、C构成△ABC，猎狗想捕捉兔子，必须到三个洞口的距离都相等，则猎狗应蹲守在（）

A、三条边的垂直平分线的交点

B、三个角的角平分线的交点

C、三角形三条高的交点

D、三角形三条中线的交点

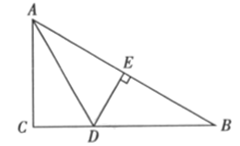
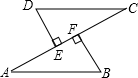
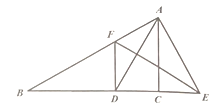
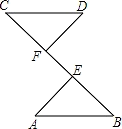
如图，BE=CF，AE⊥BC，DF⊥BC，要根据“HL”证明Rt△ABE≌Rt△DCF，则还要添加一个条件是（）

A、 AB=DC

B、 ∠A=∠D

C、 ∠B=∠C

D、 AE=BF

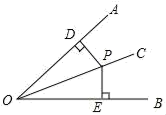
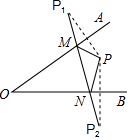
已知：如图，∠AOB内一点P，P₁ ， P₂分别P是关于OA、OB的对称点，P₁P₂交OA于M，交OB于N，若P₁P₂＝6cm，则△PMN的周长是（）

A、 3cm

B、 4cm

C、 5cm

D、 6cm

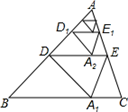
如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ，连接 $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ．下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③ $\text{[math]}$ 平分 $\text{[math]}$ ；④ $\text{[math]}$ 平分 $\text{[math]}$ ．其中正确的个数为（）．

A、 4

B、 3

C、 2

D、 1

填空题

给出下列4种图形：①线段，②等腰三角形，③平行四边形，④圆.其中，不一定是轴对称图形的是（填写序号）.

如图，BF＝EC，∠A＝∠D，那么要得到△ABC≌△DEF，可以添加一个条件（只需填上一个正确的条件.

在如图所示的2×2方格中，连接AB、AC，则∠1+∠2=度.

如果△ABC与△A'B'C'关于直线l对称，且∠A＝50°，∠B'＝70°，那么∠C'＝.

如图，已知 $\text{[math]}$ ， AD平分 $\text{[math]}$ 于点E， $\text{[math]}$ ，则BC= cm。

如图，在△ABC中，DE是BC的垂直平分线.若AC＝8cm，△ABE的周长为13cm，则AB的长为.

如图，△ABC≌△ADE，点E在BC上，若∠C＝80°，则∠DEB＝.

如图，将△ABC沿着过AB中点D的直线折叠，使点A落在BC边上的A₁ ，称为第1次操作，折痕DE到BC的距离记为h₁；还原纸片后，再将△ADE沿着过AD中点D₁的直线折叠，使点A落在DE边上的A₂处，称为第2次操作，折痕D₁E₁到BC的距离记为h₂：按上述方法不断操作下去…，经过第2019次操作后得到的折痕D₂₀₁₈E₂₀₁₈ ，到BC的距离记为h₂₀₁₉：若h₁＝1，则h₂₀₁₉的值为

解答题

如图，已知O是AB的中点，∠A＝∠B，求证：△AOC≌△BOD.

如图，AB＝CD，DE⊥AC，BF⊥AC，点E，F是垂足，AE＝CF，求证：

证明命题“角平分线上的点到角两边的距离相等”，要根据题意，画出图形，并用符号表示已知求证，写出证明过程，下面是小明同学根据题意画出的图形，并写出了不完整的已知和求证.

如图，在 $\text{[math]}$ 的正方形网格中，有格点 $\text{[math]}$ 和 $\text{[math]}$ ，且 $\text{[math]}$ 和 $\text{[math]}$ 关于某条直线成轴对称，请在下面给出的图中，画出3个不同位置的 $\text{[math]}$ 及其对称轴MN.

如图所示，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 平分线， $\text{[math]}$ 的垂直平分线分别交 $\text{[math]}$ 延长线于点 $\text{[math]}$ .求证： $\text{[math]}$ .

证明：∵ $\text{[math]}$ 平分 $\text{[math]}$

∴ $\text{[math]}$ $\text{[math]}$ (角平分线的定义)

∵ $\text{[math]}$ 垂直平分 $\text{[math]}$

∴ $\text{[math]}$ （线段垂直平分线上的点到线段两个端点距离相等）

∴ $\text{[math]}$ （）

∴ $\text{[math]}$ （等量代换）

∴ $\text{[math]}$ （）

如图，将长方形纸片ABCD折叠，使点C与点A重合，折痕EF分别与AB、DC交于点E和点F.

如图，Rt△ABC中，AB＝AC，∠BAC＝90°，直线l为经过点A的任一直线，BD⊥l于D，CE⊥l于E，若BD＞CE，试问：

如图，有一直角三角形ABC，∠C=90°，AC=10cm，BC=5cm，一条线段PQ=AB，P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动，问P点运动到AC上什么位置时△ABC才能和△APQ全等．

相关试卷推荐

友情链接

组卷网课件下载备课易 StirlingPdf 排课软件云字帖

2016-2022 组卷题库
组卷题库试题答案查询