单选题
直角三角形的两条边长为5和12,它的斜边长为( )
- A、 13
- B、
- C、 13或
- D、 13或12
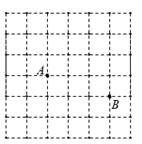
如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为( )
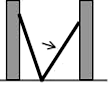
- A、 2.2米
- B、 2.3米
- C、 2.4米
- D、 2.5米
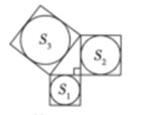
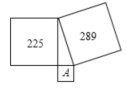
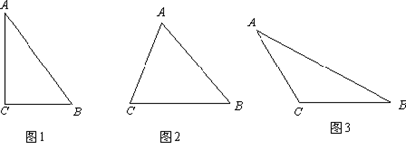
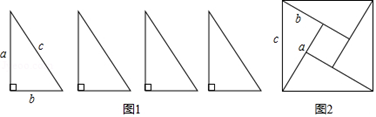
我国是最早了解勾股定理的国家之一  下面四幅图中,不能证明勾股定理的是
下面四幅图中,不能证明勾股定理的是 

- A、

- B、
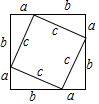
- C、
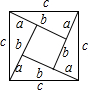
- D、

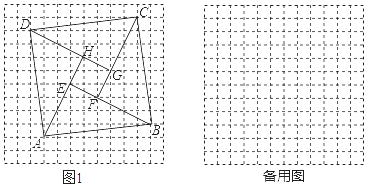
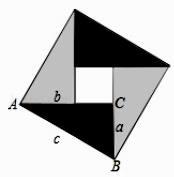
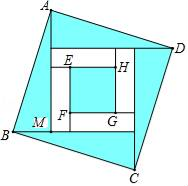
四个全等的直角三角形按图示方式围成正方形ABCD,过各较长直角边的中点作垂线,围成面积为S的小正方形EFGH.已知AM为Rt△ABM较长直角边,AM=2  EF,则正方形ABCD的面积为( )
EF,则正方形ABCD的面积为( )
- A、 14S
- B、 13S
- C、 12S
- D、 11S
三角形的三边a,b,c满足(a+b)2-c2=2ab,则此三角形是( ).
- A、 锐角三角形
- B、 直角三角形
- C、 钝角三角形
- D、 等边三角形
以a.b.c为边的三角形是直角三角的为( )
- A、 a=2,b=3,c=4
- B、 a=1,b=
,c=2
- C、 a=4,b=5,c=6
- D、 a=2,b=2,c=
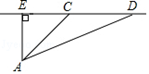
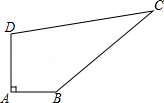
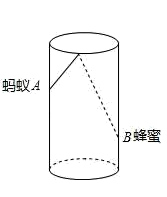
如图,圆柱形容器高为18cm,底面周长为24cm,在杯内壁离杯底4cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿2cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到达内壁B处的最短距离为( ).
- A、 13cm
- B、
cm
- C、 2
cm
- D、 20cm
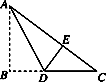
如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )
- A、 6
- B、 5
- C、 4
- D、 3
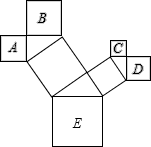
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
- A、 13
- B、 26
- C、 34
- D、 47