选择题
计算：3﹣2×（﹣1）=（ ）
- A、 5
- B、 1
- C、 ﹣1
- D、 6
下列说法正确的是（ ）
- A、 1的相反数是﹣1
- B、 1的倒数是﹣1
- C、 1的立方根是±1
- D、 ﹣1是无理数
下列运算正确的是（ ）
- A、 （
）﹣1=﹣
- B、 6×107=6000000
- C、 （2a）2=2a2
- D、 a3•a2=a5
如图所示的三视图所对应的几何体是（ ）
- A、
- B、
- C、
- D、
如图，AC，BE是⊙O的直径，弦AD与BE交于点F，下列三角形中，外心不是点O的是（ ）
- A、 △ABE
- B、 △ACF
- C、 △ABD
- D、 △ADE
在数轴上标注了四段范围，如图，则表示的点落在（ ）
- A、 段①
- B、 段②
- C、 段③
- D、 段④
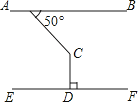
如图，AB∥EF，CD⊥EF，∠BAC=50°，则∠ACD=（ ）
- A、 120°
- B、 130°
- C、 140°
- D、 150°
利用加减消元法解方程组 
，下列做法正确的是（ ）
- A、 要消去y，可以将①×5+②×2
- B、 要消去x，可以将①×3+②×（﹣5）
- C、 要消去y，可以将①×5+②×3
- D、 要消去x，可以将①×（﹣5）+②×2
若关于x的方程x2+2x+a=0不存在实数根，则a的取值范围是（ ）.
- A、 a＜1
- B、 a＞1
- C、 a≤1
- D、 a≥1
将一质地均匀的正方体骰子掷一次，观察向上一面的点数，与点数3相差2的概率是（ ）
- A、
- B、
- C、
- D、
如图，直线l：y=﹣ 
x﹣3与直线y=a（a为常数）的交点在第四象限，则a可能在（ ）
- A、 1＜a＜2
- B、 ﹣2＜a＜0
- C、 ﹣3≤a≤﹣2
- D、 ﹣10＜a＜﹣4
如图，点A，B为定点，定直线l∥AB，P是l上一动点，点M，N分别为PA，PB的中点，对下列各值：
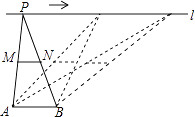
①线段MN的长；②△PAB的周长；③△PMN的面积；④直线MN，AB之间的距离；⑤∠APB的大小．
其中会随点P的移动而变化的是（ ）
- A、 ②③
- B、 ②⑤
- C、 ①③④
- D、 ④⑤
如图是甲、乙两张不同的矩形纸片，将它们分别沿着虚线剪开后，各自要拼一个与原来面积相等的正方形，则（ ）
- A、 甲、乙都可以
- B、 甲、乙都不可以
- C、 甲不可以、乙可以
- D、 甲可以、乙不可以
