初中数学浙教版九年级上册第二章简单事件的概率单元检测（提高篇）-组卷题库站

单选题

同时抛掷两枚质地均匀的正方体骰子（骰子每个面上的点数分别为1，2，3，4，5，6）．下列事件中是必然事件的是（）

A、两枚骰子朝上一面的点数和为6

B、两枚骰子朝上一面的点数和不小于2

C、两枚骰子朝上一面的点数均为偶数

D、两枚骰子朝上一面的点数均为奇数

根据你对下列诗词的理解，请你从概率统计的角度判断：所给诗词描述的事件属于随机事件的是（）

A、锄禾日当午，汗滴禾下土

B、白日依山尽，黄河入海流

C、离离原上草，一岁一枯荣

D、春眠不觉晓，处处闻啼鸟

某校九年级一班共有学生50人，现在对他们的生日（可以不同年）进行统计，则正确的说法是（　　）

A、至少有两名学生生日相同

B、不可能有两名学生生日相同

C、可能有两名学生生日相同，但可能性不大

D、可能有两名学生生日相同，且可能性很大

如图所示，电路图上有A，B，C三个开关和一个小灯泡，闭合开关C或者同时闭合开关A、B，都可使小灯泡发光．现在任意闭合其中一个开关，则小灯泡发光的概率等于（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

定义一种“十位上的数字比个位、百位上的数字都要小”的三位数叫做“V数”，如“947”就是一个“V数”.若十位上的数字为2，则从1，3，4，5中任选两数，能与2组成“V数”得概率是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

“五一”长假期间，某玩具超市设立了一个如图所示的可以自由转动的转盘，开展有奖购买活动，顾客购买玩具就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应奖品．下表是该活动的一组统计数据：

转动转盘的次数n	100	150	200	500	800	1000
落在“铅笔”区域的次数m	68	108	140	355	560	690
落在“铅笔”区域的频率 $\text{[math]}$	0.68	0.72	0.70	0.71	0.70	0.69

下列说法不正确的是（）

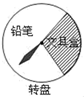
A、当n很大时，估计指针落子在”铅笔“区域的概率大约是0.70

B、假如你去转动转盘一次，获得“铅笔”概率大约是0.70

C、如果转动转盘3000次，指针落在“文具盒”区域的次数大约有900次

D、转动转盘20次，一定有6次获得“文具盒”

某学习小组做抛掷一枚纪念币的实验，整理同学们获得的实验数据，如下表．

抛掷次数	50	100	200	500	1000	2000	3000	4000	5000
“正面向上”的次数	19	38	68	168	349	707	1069	1400	1747
“正面向上”的频率	0.3800	0.3800	0.3400	0.3360	0.3490	0.3535	0.3563	0.3500	0.3494

下面有三个推断：①通过上述实验的结果，可以推断这枚纪念币有很大的可能性不是质地均匀的；②如果再次做此实验，仍按上表抛掷的次数统计数据，那么在数据表中，“正面向上”的频率有更大的可能仍会在0.35附近摆动；③在用频率估计概率时，用实验5000次时的频率0.3494一定比用实验4000次时的频率0.3500更准确．其中正确的是（）

A、 ①③

B、 ①②

C、 ②③

D、 ①②③

如图，共有12个大小相同的小正方形，其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分，现从其余的小正方形中任取一个涂上阴影，能构成这个正方体的表面展开图的概率是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

在边长为1的小正方形组成的网格中，有如图所示的A，B两点，在格点上任意放置点C，恰好能使得△ABC的面积为1的概率为（　　）.

A、

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

甲乙两人轮流在黑板上写下不超过

的正整数（每次只能写一个数），规定禁止在黑板上写已经写过的数的约数，最后不能写的为失败者，如果甲写第一个，那么，甲写数字（）时有必胜的策略．

A、 10

B、 9

C、 8

D、 6

填空题

写一个你喜欢的实数m的值，使得事件“对于二次函数 $\text{[math]}$ ，当 $\text{[math]}$ 时，y随x的增大而增大”成为随机事件，这个实数m的值.

从甲地到乙地有A，B，C三条不同的公交线路．为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况，在每条线路上随机选取了500个班次的公交车，收集了这些班次的公交车用时（单位：分钟）的数据，统计如下：

早高峰期间，乘坐（填“A”，“B”或“C”）线路上的公交车，从甲地到乙地“用时不超过45分钟”的可能性最大．

为了了解学生每月的零用钱情况，从甲、乙、丙三个学校各随机抽取200名学生，调查了他们的零用钱情况（单位：元）具体情况如下：

学校频数零用钱	100≤x＜200	200≤x＜300	300≤x＜400	400≤x＜500	500以上	合计
甲	5	35	150	8	2	200
乙	16	54	68	52	10	200
丙	0	10	40	70	80	200

在调查过程中，从（填“甲”，“乙”或“丙”）校随机抽取学生，抽到的学生“零用钱不低于300元”的可能性最大．

某水果公司新购进10000千克柑橘，每千克柑橘的成本为9元．柑橘在运输、存储过程中会有损坏，销售人员从所有的柑橘中随机抽取若干柑橘，进行“柑橘损坏率”统计，并把获得的数据记录如表所示：

柑橘总重量n/千克	50	100	150	200	250	300	350	400	450	500
损坏柑橘重量m/千克	5.50	10.50	15.15	19.42	24.25	30.93	35.32	39.24	44.57	51.54
柑橘损坏的频率 $\text{[math]}$	0.110	0.105	0.101	0.097	0.097	0.103	0.101	0.098	0.099	0.103