单选题
3×7=21,33×67=2211,333×667=222111,那么3333×6667=( )
- A、 222111
- B、 22221111
- C、 2221111
观察下面的算式:
5×9=45
55×99=5445
555×999=554445
5555×9999=55544445
则555555×999999=( )
- A、 55555444445
- B、 55554444445
- C、 555554444445
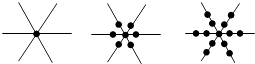
根据下面几幅图的排列规律,第四幅图是( )

- A、

- B、
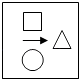
- C、
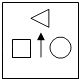
- D、

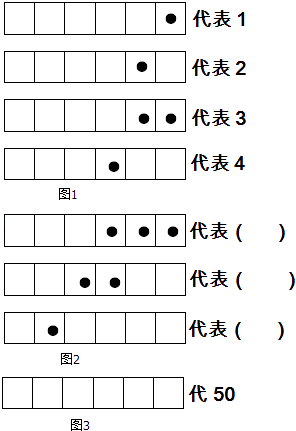
按如下规律摆放三角形:
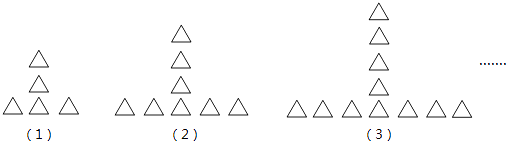
则第(5)堆三角形的个数为( )
- A、 14
- B、 15
- C、 16
- D、 17
法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”是一样的,后面的就改用手势了.如图两个图框是用法国“小九九”计算7×8和8×9的两个示例.若用法国的“小九九”计算7×9,左、右手依次伸出手指的个数是( )

- A、 2,3
- B、 3,3
- C、 2,4
- D、 3,4
古希腊著名的毕达哥拉斯学派把1、3、6、10…这样的数称为“三角形数”,而把1、4、9、16…这样的数称为“正方形数”,从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是( )

- A、 13=3+10
- B、 25=9+16
- C、 36=15+21
- D、 49=18+31