单选题
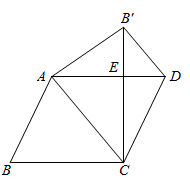
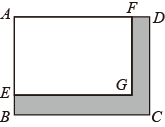
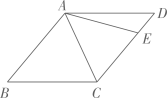
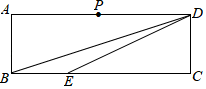
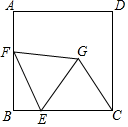
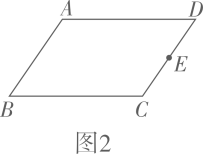
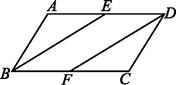
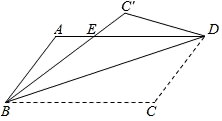
如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设  ,则
,则  为( )
为( )
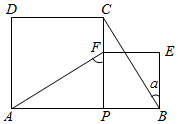
- A、 2α
- B、 90°﹣α
- C、 45°+α
- D、 90°﹣
α
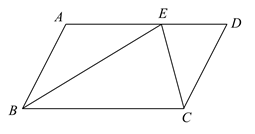
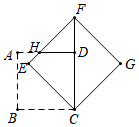
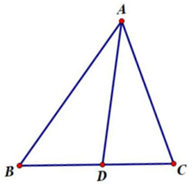
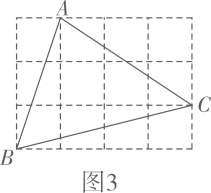
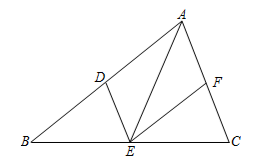
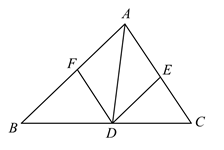
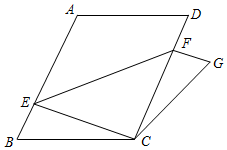
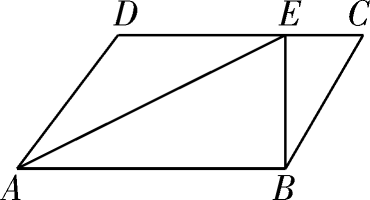
如图,D、E、F分别是  各边中点,则以下说法错误的是( )
各边中点,则以下说法错误的是( )

- A、
和
的面积相等
- B、 四边形
是平行四边形
- C、 若
,则四边形
是菱形
- D、 若
,则四边形
是矩形
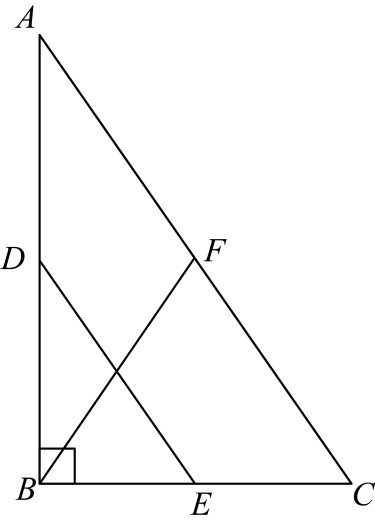
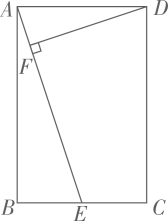
折叠矩形纸片ABCD,使点B落在点D处,折痕为MN,已知AB=8,AD=4,则MN的长是( )
- A、
- B、 2
- C、
- D、 4
正五边形的内角和是( )
- A、
- B、
- C、
- D、
正十边形的每一个外角的度数为( )
- A、
- B、
- C、
- D、
下列条件中,能判定▱ABCD是菱形的是( )
- A、 AC=BD
- B、 AB⊥BC
- C、 AD=BD
- D、 AC⊥BD
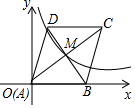
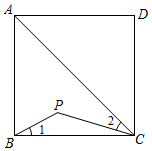
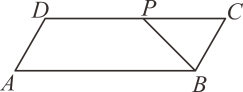
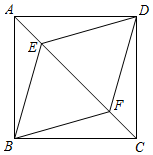
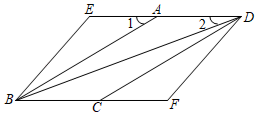
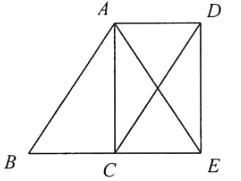
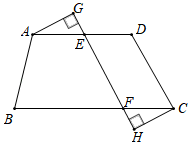
如图,在菱形  中,对角线
中,对角线  相交于点
相交于点  为
为  中点,
中点,  .则线段
.则线段  的长为:( )
的长为:( )

- A、
- B、
- C、 3
- D、 5
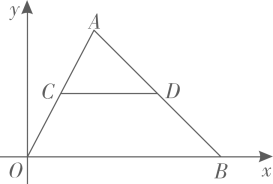
如图,小明从点A出发沿直线前进10米到达点B,向左转  后又沿直线前进10米到达点C,再向左转
后又沿直线前进10米到达点C,再向左转  后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )
后沿直线前进10米到达点D……照这样走下去,小明第一次回到出发点A时所走的路程为( )
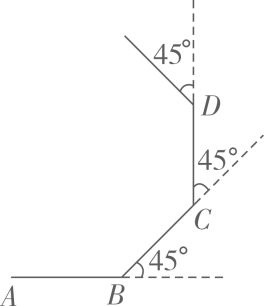

- A、 100米
- B、 80米
- C、 60米
- D、 40米
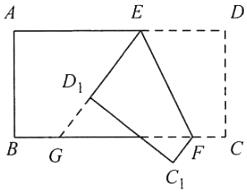
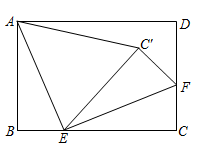
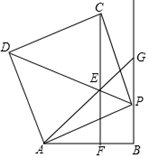
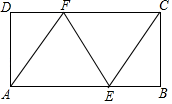
如图,将矩形纸片  沿
沿  折叠,使点A落在对角线
折叠,使点A落在对角线  上的
上的  处.若
处.若  ,则
,则  等于( ).
等于( ).
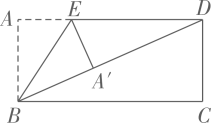
- A、
- B、
- C、
- D、
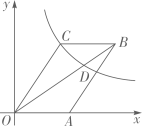
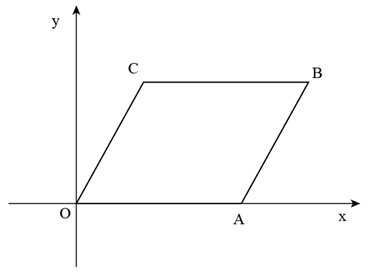
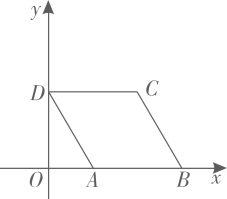
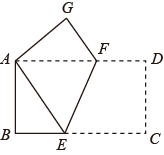
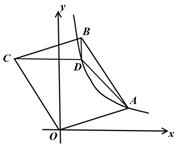
如图,点D是  内一点,
内一点,  与x轴平行,
与x轴平行,  与y轴平行,
与y轴平行,  .若反比例函数
.若反比例函数  的图像经过A、D两点,则k的值是( )
的图像经过A、D两点,则k的值是( )
- A、
- B、 4
- C、
- D、 6
下列结论中,矩形具有而菱形不一定具有的性质是( )
- A、 内角和为360°
- B、 对角线互相平分
- C、 对角线相等
- D、 对角线互相垂直