人教版数学九年级图形的认识专题训练

日期: 2025-03-30 二轮复习来源：出卷网

单选题

下列长度的三条线段能组成三角形的是（）

A、 3cm，5cm，6cm

B、 3cm，3cm，6cm

C、 3cm，4 cm，8cm

D、 4cm，5cm，1cm

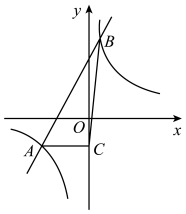
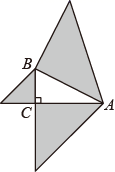
如图．AB=AC，BD=1，BD⊥AD，则数轴上点C所表示的数为（）

A、 $\text{[math]}$ +1

B、 - $\text{[math]}$ -1

C、 - $\text{[math]}$ +1

D、 $\text{[math]}$ -1

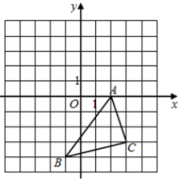
如图，在△ABC中，AB=AC，BE=CD，BD=CF，若∠A=40°，则∠EDF等于（）

A、 40°

B、 50°

C、 60°

D、 70°

如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ 是弦， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

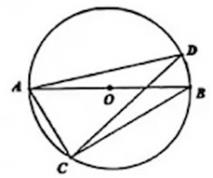
如图，P为正六边形 $\text{[math]}$ 边上一动点，点P从点D出发，沿六边形的边以1cm/s的速度按逆时针方向运动，运动到点C停止.设点P的运动时间为 $\text{[math]}$ ，以点P、C、D为顶点的三角形的面积是 $\text{[math]}$ ，则下列图象能大致反映y与x的函数关系的是（）

A、

B、

C、

D、

如图，以 $\text{[math]}$ 的三边为直角边分别向外作等腰直角三角形.若 $\text{[math]}$ ，则图中阴影部分的面积为（　　）

A、 3

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

如图，点B，C，E在同一直线上，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，下列结论不一定成立的是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

下列图形经过折叠可以围成一个棱柱的是（）

A、

B、

C、

D、

如图，在△ABC中，∠C＝90°，AB＝5，AC＝4，则tanB的值是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

如图，在OA，OB上分别截取OD，OE使OD＝OE，再分别以点D、E为圆心，大于 $\text{[math]}$ DE长为半径作弧，两弧在∠AOB内交于点C，射线OC就是∠AOB的角平分线.理由是连结CD，CE，证△COD≌△COE得∠COD＝∠COE.证△COD≌△COE的条件是（）

A、 SAS

B、 AAS

C、 ASA

D、 SSS

填空题

等腰三角形的一边长是2cm，另一边长是4cm，则底边长为cm.

如图， $\text{[math]}$ 与 $\text{[math]}$ 中，已知， $\text{[math]}$ ，请你添加一个条件（不添加字母和辅助线），使 $\text{[math]}$ ，你添加的条件是.

圆锥底面圆的半径为2cm，其侧面展开图的圆心角是180°，则圆锥的侧面积是 $\text{[math]}$ .

如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ， $\text{[math]}$ ，点D到 $\text{[math]}$ 的距离为5.6，则 $\text{[math]}$ $\text{[math]}$ .

如图，点 A 、 B 、 P 是⊙ O 上的三点，若AOB ＝50°，则APB 的度数为．

如图，已知一次函数y＝2x+4的图象与反比例函数 $\text{[math]}$ 的图象交于A，B两点，点B的横坐标是1，过点A作AC⊥y轴于点C，连接BC，则△ABC的面积是．

作图题

如图，在直角坐标系中，将△ABC绕点A顺时针旋转90°．

解答题

完成下面的证明

如图，点B在AG上，AG $\text{[math]}$ CD，CF平分∠BCD，∠ABE＝∠FCB，BE⊥AF点E．

求证：∠F＝90°．

证明：∵AG $\text{[math]}$ CD（已知）

∴∠ABC＝∠BCD（ ▲ ）

∵∠ABE＝∠FCB（已知）

∴∠ABC﹣∠ABE＝∠BCD﹣∠FCB

即∠EBC＝∠FCD

∵CF平分∠BCD（已知）

∴∠BCF＝∠FCD（ ▲ ）

∴ ▲ ＝∠BCF（等量代换）

∴BE $\text{[math]}$ CF（ ▲ ）

∴ ▲ ＝∠F（ ▲ ）

∵BE⊥AF（已知）

∴ ▲ ＝90°（ ▲ ）

∴∠F＝90°．

如图，在 $\text{[math]}$ 中， $\text{[math]}$ 为 $\text{[math]}$ 的高， $\text{[math]}$ 为 $\text{[math]}$ 的角平分线， $\text{[math]}$ 交 $\text{[math]}$ 于点G， $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的大小.

如图，已知点E、C在线段BF上， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .求证：

如图，AB为 $\text{[math]}$ 的直径，点C，D在 $\text{[math]}$ 上， $\text{[math]}$ ， $\text{[math]}$ ．求证：DE是 $\text{[math]}$ 的切线．

相关试卷推荐

友情链接

组卷网课件下载备课易 StirlingPdf 排课软件云字帖

2016-2022 组卷题库
组卷题库试题答案查询