2021-2022学年度第二学期七年级数学第五章《相交线与平行线》5.3平行线的性质课堂练习卷

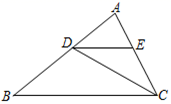
如图，AD∥BC，∠C＝30°，∠ADB：∠BDC＝1：2，∠EAB＝72°，以下四个说法：

①∠CDF＝30°；②∠ADB＝50°；

③∠ABD＝22°；④∠CBN＝108°

其中正确说法的个数是（  ）

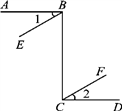
如图，AB∥CD，AE∥CF，∠A=41°，则∠C的度数为（   ）

如图，直线AB∥CD，直线AB、CD被直线EF所截，交点分别为点M、点N，若∠AME＝130°，则∠DNM的度数为（       ）

如图，直尺的一条边经过直角三角尺的直角顶点且平分直角，它的对边恰巧经过60°角的顶点．则∠1的大小是（   ）

如图，已知AD//BC，∠B=32°，DB平分∠ADE，则∠DEC=（  ）

下列选项中，可以用来证明命题“若a>b，则|a|>|b|”是假命题的反例是（    ）

能说明命题“对于任意实数a，都有a²＞0”是假命题的反例是（   ）

下列说法不正确的是（     ）

下列说法中，错误的是（    ）

下列结论中，正确的是（    ）

一艘旅游船从 点出发沿北偏东 方向航行，到达 景点后，进行了 的转弯，然后沿着 方向航行，则 为方向．

如图， ， 平分 ， ， 则．

如图，AB∥CD∥EF，若∠ABC＝125°，∠CEF＝105°，则∠BCE的度数为 ．

若要证明命题“若a²>1，则a>1”是假命题，则可以举一个反例是。

命题“a＜2a”是 命题（填“真”或“假”）.

如图，已知DE∥BC，BE是∠ABC的平分线，∠C=70°，∠ABC=50°．求∠DEB和∠BEC的度数．

根据解答过程填空（写出推理理由或数学式）：

如图，已知∠DAF＝∠F，∠B＝∠D，试说明AB∥DC．

证明：∵∠DAF＝∠F（已知）．

∴AD∥BF（                  ▲                        ），

∴∠D＝∠DCF（                   ▲                        ）．

∵∠B＝∠D（已知），

∴（                  ▲                        ）＝∠DCF（等量代换），

∴AB∥DC（                   ▲                        ）．

如图，如果∠1＝60°，∠2＝120°，∠D＝60°，那么AB与CD平行吗？BC与DE呢？

观察下面的解答过程，补充必要的依据或结论．

解∵∠1＝60°（已知）

∠ABC＝∠1 （①            ▲                  ）

∴∠ABC＝60°（等量代换）

又∵∠2＝120°（已知）

∴（②                  ▲                        ）+∠2＝180°（等式的性质）

∴AB∥CD （③                  ▲                        ）

又∵∠2+∠BCD＝（④            ▲                  °）

∴∠BCD＝60°（等式的性质）

∵∠D＝60°（已知）

∴∠BCD＝∠D （⑤                        ▲                  ）

∴BC∥DE （⑥                  ▲                        ）

如图，已知AB∥DE，∠1=18°，∠2=125°，求∠BCD的度数．

下列命题中，哪些是真命题？哪些是假命题？

①内错角相等；

②两直线平行，同旁内角互补；

③若x=2，则x+1>1；

④不等式两边同时乘以或除以一个负数，不等号应改变方向；

⑤三角形两边之和大于第三边．

如图，直线AB和直线CD，直线BE和直线CF都被直线BC所截．在下面三个条件中，请你选择其中两个作为题设，剩下的一个作为结论，组成一个真命题并证明．

①AB⊥BC，CD⊥BC，②BE∥CF，③∠1＝∠2.

“定义、定理、基本事实、命题、真命题、假命题”它们之间的关系恰好可以用下图表示，请指出A，B，C，D，E，F分别与它们中的哪一个对应．