山西省2022年中考数学真题-组卷题库站

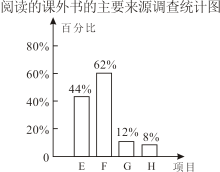
单选题

实数－6的相反数是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、－6

D、 6

2022年4月16日，神舟十三号载人飞船圆满完成全部既定任务，顺利返回地球家园．六个月的飞天之旅展现了中国航天科技的新高度下列航天图标，其文字上方的图案是中心对称图形的是（）

A、

B、

C、

D、

粮食是人类赖以生存的重要物质基础，2021年我国粮食总产量再创新高，达68285万吨．该数据可用科学记数法表示为（）

A、 $\text{[math]}$ 吨

B、 $\text{[math]}$ 吨

C、 $\text{[math]}$ 吨

D、 $\text{[math]}$ 吨

神奇的自然界处处蕴含着数学知识．动物学家在鹦鹉螺外壳上发现，其每圈螺纹的直径与相邻螺纹直径的比约为0.618．这体现了数学中的（）

A、平移

B、旋转

C、轴对称

D、黄金分割

不等式组 $\text{[math]}$ 的解集是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

如图， $\text{[math]}$ 是一块直角三角板，其中 $\text{[math]}$ ．直尺的一边DE经过顶点A，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

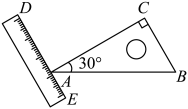
A、 100°

B、 120°

C、 135°

D、 150°

化简 $\text{[math]}$ 的结果是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

如图， $\text{[math]}$ 内接于 $\text{[math]}$ ， AD是 $\text{[math]}$ 的直径，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A、 60°

B、 65°

C、 70°

D、 75°

“二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界普为“中国第五大发明”，小文购买了“二十四节气”主题邮票，他要将“立春”“立夏”“秋分”“大赛”四张邮票中的两张送给好朋友小乐．小文将它们背面朝上放在桌面上（邮票背面完全相同），让小乐从中随机抽取一张（不放回），再从中随机抽取一张，则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

如图，扇形纸片AOB的半径为3，沿AB折叠扇形纸片，点O恰好落在 $\text{[math]}$ 上的点C处，图中阴影部分的面积为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

填空题

计算 $\text{[math]}$ 的结果是．

根据物理学知识，在压力不变的情况下，某物体承受的压强 $\text{[math]}$ 是它的受力面积 $\text{[math]}$ 的反比例函数，其函数图象如图所示，当 $\text{[math]}$ 时，该物体承受的压强p的值为 Pa．

生物学研究表明，植物光合作用速率越高，单位时间内合成的有机物越多，为了解甲、乙两个品种大豆的光合作用速率，科研人员从甲、乙两个品种的大豆中各选五株，在同等实验条件下，测量它们的光合作用速率（单位： $\text{[math]}$ ），结果统计如下：

品种	第一株	第二株	第三株	第四株	第五株	平均数
甲	32	30	25	18	20	25
乙	28	25	26	24	22	25

则两个大豆品种中光合作用速率更稳定的是（填“甲”或“乙”）．

某品牌护眼灯的进价为240元，商店以320元的价格出售．“五一节”期间，商店为让利于顾客，计划以利润率不低于20%的价格降价出售，则该护眼灯最多可降价元．

如图，在正方形ABCD中，点E是边BC上的一点，点F在边CD的延长线上，且 $\text{[math]}$ ，连接EF交边AD于点G．过点A作 $\text{[math]}$ ，垂足为点M，交边CD于点N．若 $\text{[math]}$ ， $\text{[math]}$ ，则线段AN的长为

解答题

如图，在矩形ABCD中，AC是对角线．

2022年我国已成为全球最大的电动汽车市场，电动汽车在保障能源安全，改善空气质量等方面较传统汽车都有明显优势，经过对某款电动汽车和某款燃油车的对比调查发现，电动汽车平均每公里的充电费比燃油车平均每公里的加油费少0.6元．若充电费和加油费均为200元时，电动汽车可行驶的总路程是燃油车的4倍，求这款电动汽车平均每公里的充电费．

首届全民阅读大会于2022年4月23日在北京开幕，大会主题是“阅读新时代·奋进新征程”．某校“综合与实践”小组为了解全校3600名学生的读书情况，随机抽取部分学生进行问卷调查，形成了如下调查报告（不完整）：

××中学学生读书情况调查报告

调查主题	××中学学生读书情况
调查方式	抽样调查		调查对象	××中学学生
数据的收集、整理与描述	第一项	您平均每周阅读课外书的时间大约是（只能单选，每项含最小值，不含最大值） A.8小时及以上； B.6～8小时； C.4～6小时； D.0～4小时．
	第二项	您阅读的课外书的主要来源是（可多选） E．自行购买； F．从图书馆借阅； G．免费数字阅读； H．向他人借阅．
调查结论	……

请根据以上调查报告，解答下列问题：

阅读与思考

下面是小宇同学的数学小论文，请仔细阅读并完成相应的任务

用函数观点认识一元二次方程根的情况

我们知道，一元二次方程 $\text{[math]}$ 的根就是相应的二次函数 $\text{[math]}$ 的图象（称为抛物线）与x轴交点的横坐标．抛物线与x轴的交点有三种情况：有两个交点、有一个交点、无交点．与此相对应，一元二次方程的根也有三种情况：有两个不相等的实数根、有两个相等的实数根、无实数根．因此可用抛物线与x轴的交点个数确定一元二次方程根的情况