四川省达州市渠县2021-2022学年七年级下学期期末数学试卷-组卷题库站

单选题

甲骨文是我国古代的一种文字，是汉字的早期形式，反映了我国悠久的历史文化，体现了我国古代劳动人民的智慧，下列甲骨文中，不是轴对称图形的是（　　）

A、

B、

C、

D、

若a为正整数，则 $\text{[math]}$ =（）

A、 a^2a

B、 2a^a

C、 a^a

D、 $\text{[math]}$

奥密克戎是新型冠状病毒的一种变异株，它给全球人民带来了巨大的灾难，冠状病毒的直径约80﹣120nm，1nm为十亿分之一米，即 $\text{[math]}$ m，将95nm用科学记数法表示正确的是（）米.

A、 9.5× $\text{[math]}$

B、 9.5× $\text{[math]}$

C、 95× $\text{[math]}$

D、 0.95× $\text{[math]}$

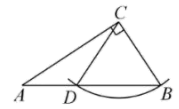
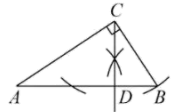
木工师傅将一把三角尺和一个重锤如图放置，就能检查一根横梁是否水平，能解释这一现象的数学知识是（）

如图，AB//CD，EF＝DF，若∠A＝50°，则∠E 等于（）

如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．用无刻度的直尺和圆规在AB边上找一点D，使 $\text{[math]}$ ，则符合要求的作图是（）

B、投掷一枚质地均匀的硬币1000次，正面朝上的次数一定是500次

C、从1、2、3、4、5中任取一个数是偶数的可能性比较大

D、 13名同学中，至少有两人的出生月份相同是必然事件

若一个等腰三角形的周长为32，则该等腰三角形的腰长x的取值范围是（）

已知A、B两地相距600米，甲、乙两人同时从A地出发前往B地，所走路程y（米）与行驶时间x（分）之间的函数关系如图所示，则下列说法中：①甲每分钟走100米；②2分钟后，乙每分钟走50米；③甲比乙提前3分钟到达B地；④当x=2或6时，甲乙两人相距100米.其中，正确的是（）

填空题

一辆汽车以70km/h的速度在高速路上匀速行驶，则该汽车行驶的路程S（km）与时间t（h）之间的关系式是，其中自变量是，因变量是.

大数据分析技术为打赢疫情防控阻击战发挥了重要作用，如图是张老师的健康码示意图，用黑白打印机打印在边长为2cm的正方形区域内，图中黑色部分的总面积为2.4cm² ，现在向正方形区域内随机掷点，点落入黑色部分的概率为.

如图，爱思考的小红观看舞蹈时，发现某一时刻的情形抽象成数学问题：如图，已知AB $\text{[math]}$ CD，∠BAE=93°，∠DCE=116°，则∠E的度数是.

若 $\text{[math]}$ ，则 $\text{[math]}$ .

小芳和小林为了研究图中“跑到画板外面去的两直线a，b所成的角（锐角）”问题，设计出如下两个方案：

现在小林只测得∠β=115°，小芳作了AB=BC，并只测得∠1=80°，请你根据以上信息求出直线a，b所成角的度数.

如图，等腰直角△ABC中，∠BAC=90°，AD $\text{[math]}$ BC于D，∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，延长AM交BC于点N，连接DM，NE.下列结论：①AE=AF；②AM⊥EF；③△AEF是等边三角形；④DF=DN；⑤AD $\text{[math]}$ EN.其中正确的结论有.

解答题

计算

先化简，再求值 $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ .

如图，在正方形网格中，△ABC的顶点都在格点上，∠ACB=90°，AC=BC，点C在直线MN上，请完成下列问题：

如图，在△ABC中，AC=BC，∠B=42°，点D是边AB上一点，点B关于直线CD的对称点为 $\text{[math]}$ ，当 $\text{[math]}$ $\text{[math]}$ AC时，求∠BCD的度数.

课堂上老师给了一个问题：

已知：如图，AB $\text{[math]}$ CD，EF $\text{[math]}$ AB于点O，FG交CD于点P，当∠1=30°时，求∠EFG的度数.

同学们讨论后，发现解决此问题有多种思路：思路一：过点F作MN $\text{[math]}$ CD（如图（1））；

思路二：过点P作PN $\text{[math]}$ EF，交AB于点N.......；

按要求解答下列问题：

【数学试验】

数学学习小组在学习“用频率估计概率”的数学活动课上，做投掷骰子（质地均匀的正方体）试验，他们共做了100次试验，试验的结果如下：

向上点数	1	2	3	4	5	6
出现次数	12	19	15	18	20	x

完全平方公式：（a±b）²=a²±2ab+b² ，适当的变形，可以解决很多的数学问题.例如：若a+b=3，ab=1，求a²+b²的值.

解：因为a+b=3，

所以（a+b）²=9，即：a²+2ab+b²=9，又因为ab=1

所以a²+b²=7

根据上面的解题思路与方法，解决下列问题：

∠MON=90°，点A，B分别在OM、ON上运动（不与点O重合）.

问题发现：如图1，∠AOB=90°，OC平分∠AOB，把三角尺的直角顶点落在OC的任意一点P上，并使三角尺的两条直角边分别与OA、OB相交于点E、F.探究发现PE=PF（可以这样想：作PM $\text{[math]}$ OA于点M，PN $\text{[math]}$ OB于点N，易得PM=PN，∠PME=∠PNF=90°，∠MPE=∠NPF=90°-∠EPN，所以△PNM $\text{[math]}$ △PNF，所以PE=PF）

变式拓展：如图2，已知∠AOB=120°，OC平分∠AOB，P是OC上一点，∠EPF=60°，PE边与OA边相交于点E，PF边与射线OB的反向延长线相交于点F.

四川省达州市渠县2021-2022学年七年级下学期期末数学试题