单选题
已知一个正多边形的内角是140°,则它是几边形( )
- A、 10
- B、 9
- C、 8
- D、 7
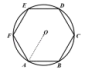
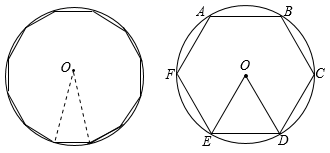
如图,若正六边形  绕着中心
绕着中心  旋转角
旋转角  得到的图形与原来的图形重合,则
得到的图形与原来的图形重合,则  最小值为( )
最小值为( )

- A、

- B、

- C、

- D、

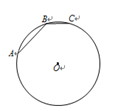
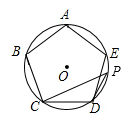
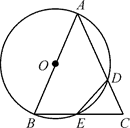
如图, 是半圆的直径,
是半圆的直径, 、
、 是半圆上的两点,
是半圆上的两点, , 则
, 则 ( )
( )
- A、 55°
- B、 65°
- C、 75°
- D、 85°
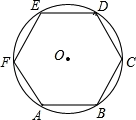
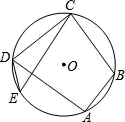
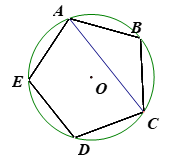
如图,正五边形ABCDE内接于⊙O,连接AC,则∠ACD的度数是 ( )
- A、 72°
- B、 70°
- C、 60°
- D、 45°
⊙O半径为4,以⊙O的内接正三角形、正方形、正六边形的边心距为边作一个三角形,则所得三角形的面积是( )
- A、 2
- B、
- C、 2
- D、 2
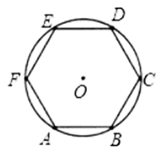
如图,正六边形ABCDEF的半径 , 则点B的坐标为( )
, 则点B的坐标为( )

- A、
- B、
- C、
- D、
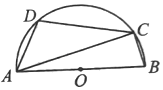
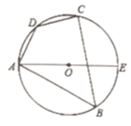
如图,AE是四边形ABCD外接圆 的直径,
的直径, ,
,  , 则
, 则 的度数为( )
的度数为( )
- A、 50°
- B、 55°
- C、 60°
- D、 65°
如图,D是等边△ABC外接圆  上的点,且∠CAD=20°,则∠ACD的度数为( )
上的点,且∠CAD=20°,则∠ACD的度数为( )

- A、 20°
- B、 30°
- C、 40°
- D、 45°