单选题
下面属于中心投影的是( )
- A、 太阳光下的树影
- B、 皮影戏
- C、 月光下房屋的影子
- D、 海上日出
当棱长为20的正方体的某个面平行于投影面时,这个面的正投影的面积为( )
- A、 20
- B、 300
- C、 400
- D、 600
小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵随太阳转动的情况,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为( )
- A、 上午12时
- B、 上午10时
- C、 上午9时30分
- D、 上午8时
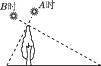
一天上午小红先参加了校运动会女子100m比赛,过一段时间又参加了女子400m比赛,如图是摄影师在同一位置拍摄的两张照片,那么下列说法正确的是( )

- A、 乙照片是参加100 m的
- B、 甲照片是参加400 m的
- C、 乙照片是参加400 m的
- D、 无法判断甲、乙两张照片
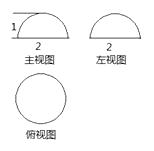
如图所示的几何体的主视图是( )

- A、

- B、

- C、

- D、

如图所示的几何体的俯视图是( )

- A、
- B、

- C、

- D、

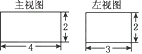
如图是某几何体的三视图,这个几何体可以是( )

- A、

- B、

- C、

- D、

某正方体的每个面上都有一个汉字,它的一个展开图如图说是,正原正方体中,与“考”字所在面相对的面上的汉字是( )

- A、 祝
- B、 你
- C、 成
- D、 功
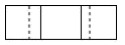
一个几何体的展开图如图所示,这个几何体是( )

- A、 三棱柱
- B、 三棱锥
- C、 四棱柱
- D、 四棱锥
如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )

- A、 0,1,﹣2
- B、 1,0,﹣2
- C、 ﹣2,0,1
- D、 0,﹣2,1