单选题
实数 中, 最小的数是( )
中, 最小的数是( )
- A、
- B、 0
- C、
- D、 2
已知 的半径为5 , 若
的半径为5 , 若 , 则点
, 则点 在( )
在( )
- A、 圆内
- B、 圆上
- C、 圆外
- D、 无法判断
任意抛掷一枚均匀的骰子, 结果朝上一面的点数为2的倍数的概率是( )
- A、
- B、
- C、
- D、
把抛物线 向下平移1个单位, 所得拋物线的表达式为( )
向下平移1个单位, 所得拋物线的表达式为( )
- A、
- B、
- C、
- D、
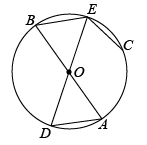
如图, 是
是 的半径, 以
的半径, 以 为直径的
为直径的 与
与 的弦
的弦 相交于点
相交于点 , 则
, 则 与
与 的大小关系( )
的大小关系( )

- A、
- B、
- C、
- D、 无法判断
已知二次函数 的部分图象如图所示, 若
的部分图象如图所示, 若 , 则
, 则 的取值的范围是( )
的取值的范围是( )

- A、
- B、
或
- C、
- D、
一个袋子中装有12个球 (袋中每个球除颜色外其余都相同). 某活动小组想估计袋子中红球的个数, 分10个组进行摸球试验, 每一组做400次试验, 汇总后, 摸到红球的次数为 3000次. 请你估计袋中红球接近( )
- A、 3
- B、 4
- C、 6
- D、 9
如图, 将抛物线 沿
沿 轴翻折, 翻折前后的两条抛物线构成一个新图象.若直线
轴翻折, 翻折前后的两条抛物线构成一个新图象.若直线 与这个新图象有3个公共点, 则
与这个新图象有3个公共点, 则 的值为( )
的值为( )

- A、
或2
- B、
或2
- C、 2或4
- D、
或4