单选题
小明和他的爸爸妈妈共三人站成一排拍照,他的父母不相邻的概率是( )
- A、
- B、
- C、
- D、
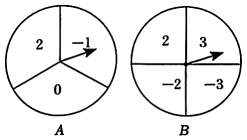
已知 是平面直角坐标系
是平面直角坐标系 中的点, 其中
中的点, 其中 是从1, 2,3三个数中任取的一个数,
是从1, 2,3三个数中任取的一个数,  是从1, 2 , 3,4四个数中任取的一个数. 定义“点
是从1, 2 , 3,4四个数中任取的一个数. 定义“点 在直线
在直线 上”为事件
上”为事件 为整数), 则当
为整数), 则当 的概率最大时,
的概率最大时,  的所有可能的值为( )
的所有可能的值为( )
- A、 5
- B、 4 或 5
- C、 5 或 6
- D、 4 或 6
有两辆车按1,2编号,方方和成成两人可以任意选坐一辆车,则两人同坐1号车的概率为( )
- A、
- B、
- C、
- D、