初中数学同步训练必刷题（北师大版七年级下册1. 4 整式的乘法）

作者UID:3629939

日期: 2024-12-25

同步测试

单选题

计算：（﹣a²b）²•a²＝（）

下列运算正确的是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A、 $\text{[math]}$

D、 $\text{[math]}$

若x²-bx-10=（x+5）（x-a），则a^b的值是（）

C、 $\text{[math]}$

D、 $\text{[math]}$

若x+m与x﹣5的乘积中不含x的一次项，则m的值是（）

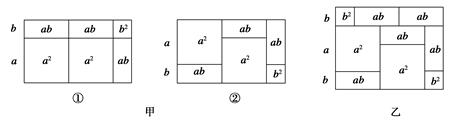
如图所示的正方形和长方形卡片各有若干张，若要拼成一个长为 $\text{[math]}$ ，宽为 $\text{[math]}$ 的长方形，则需要 $\text{[math]}$ 类， $\text{[math]}$ 类， $\text{[math]}$ 类卡片各（）张.

若x²－ax－5＝(x－5)(x＋1)，则a为（）

从前，古希腊一位庄园主把一块长为a米，宽为b米（ $\text{[math]}$ ）的长方形土地租给租户张老汉，第二年，他对张老汉说：“我把这块地的长增加10米，宽减少10米.维续租给你，租金不变，你也没有吃亏，你看如何？”如果这样，你觉得张老汉的租地面积会（）

C、没有变化

D、无法确定

已知 $\text{[math]}$ 都是正数，如果（） $\text{[math]}$ $\text{[math]}$ ，那么 $\text{[math]}$ 的大小关系是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

填空题

计算： $\text{[math]}$ =.

计算： $\text{[math]}$ ．

计算： $\text{[math]}$ ．

若 $\text{[math]}$ ，则 $\text{[math]}$ ．

如果 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ =.

已知 $\text{[math]}$ 展开式中不含 $\text{[math]}$ 项，且 $\text{[math]}$ 的系数为2．则 $\text{[math]}$ 的值为．

若m，n为常数，等式（x+2）（x-1）=x²+mx+n恒成立，则mⁿ的值为．

已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值是 .

已知计算xⁿ·（xⁿ+x²-1）的结果是一个六次多项式，则n=.

观察图，写出此图可以验证的一个等式．（写出一个即可）

解答题

阅读下列文字，并解决问题。

已知x²y=3，求2xy（x⁵y²-3x³y-4x）的值.

分析：考虑到满足x²y=3的x，y的可能值较多，不可以逐一代入求解，故考虑整体思想，将x²y=3整体代入.

解：2xy（x⁵y²-3x³y-4x）

=2x⁶y³-6x⁴y²-8x²y

=2（x²y）³-6（x²y）²-8x²y，

将x²y=3代入

原式=2×3³-6×3²-8×3=-24.

请你用上述方法解决下面问题：

已知ab=3，求（2a³b²-3a²b+4a）·（-2b）的值.

已知二次三项式 $\text{[math]}$ 与多项式 $\text{[math]}$ （a、b为常数）相乘，积中不出现二次项，且一次项系数为 $\text{[math]}$ ，求 $\text{[math]}$ 、 $\text{[math]}$ 的值．

甲、乙两人共同计算一道整式： $\text{[math]}$ ．由于甲抄错了 $\text{[math]}$ 的符号，得到的结果是 $\text{[math]}$ ，乙漏抄了第二个多项式中 $\text{[math]}$ 的系数，得到的结果是 $\text{[math]}$ ．求 $\text{[math]}$ 的值．

阅读材料：

在学习多项式乘以多项式时，我们知道 $\text{[math]}$ 的结果是一个多项式，并且最高次项为： $\text{[math]}$ ，常数项为： $\text{[math]}$ ．那么一次项是多少呢？

要解决这个问题，就是要确定该一次项的系数．通过观察，我们发现：一次项系数就是： $\text{[math]}$ ，即一次项为 $\text{[math]}$ ．

参考材料中用到的方法，解决下列问题：

阅读材料并解答下列问题.

你知道吗？一些代数恒等式可以用平面图形的面积来表示，例如（2a＋b）（a＋b）＝2a²＋3ab＋b²就可以用图甲中的①或②的面积表示.

试卷列表

教育网站链接

在线组卷课件下载评课网课件工坊 PPT模板排课软件云字帖