单选题(每题3分,共30分)
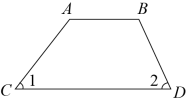
在如下所示的条件中,可以判断两条直线互相垂直的是( )
①两直线相交所成的四个角都是直角;②两直线相交,对顶角互补;③两直线相交所成的四个角都相等.
- A、 ①②
- B、 ①③
- C、 ②③
- D、 ①②③
三条直线a、b、C,若a∥c,b∥c,则a与b的位置关系是( )
- A、 a⊥b
- B、 a∥b
- C、 a⊥b或a∥b
- D、 无法确定
下列现象中,不属于平移的是( )
- A、 滑雪运动员在平坦的雪地上沿直线滑行
- B、 时针的走动
- C、 商场自动扶梯上顾客的升降运动
- D、 火车在笔直的铁轨上行驶
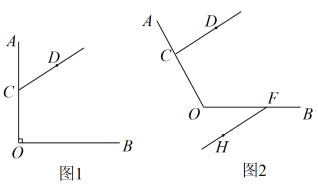
如下图,直线AD、BE被直线BF和AC所截,下列说法正确的是( )

- A、 ∠3与∠4是同旁内角
- B、 ∠2与∠5是同位角
- C、 ∠6与∠1是内错角
- D、 ∠2与∠6是同旁内角
下列说法错误的是( )
- A、 对顶角相等
- B、 同位角相等
- C、 同角的余角相等
- D、 同角的补角相等
如图,∠1和∠2是同位角的是( ).
- A、

- B、

- C、

- D、

如下图,下列条件能判断两直线AB,CD平行的是( )

- A、 ∠1=∠2
- B、 ∠3=∠4
- C、 ∠1=∠5
- D、 ∠3=∠5
如图,给出了过直线外一点作已知直线的平行线的方法,其依据是( )
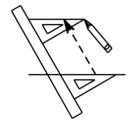
- A、 两直线平行,同旁内角相等
- B、 内错角相等,两直线平行
- C、 同旁内角互补,两直线平行
- D、 同位角相等,两直线平行
如图,AB∥CD,CB平分∠ABD.若∠C=40°,则∠D的度数为( )
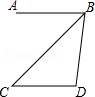
- A、 90°
- B、 100°
- C、 110°
- D、 120°
下列图形中,根据 , 能得到
, 能得到 的是( )
的是( )
- A、
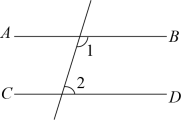
- B、

- C、

- D、