选择题
下列长度的各组线段能组成一个三角形的是( )
- A、
- B、
- C、
- D、
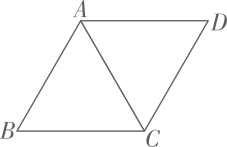
第二十四届国际数学家大会会徽的设计基础是1700多年前中国古代数学家赵爽的“弦图”.如图,在由四个全等的直角三角形( )和中间一个小正方形
)和中间一个小正方形 拼成的大正方形
拼成的大正方形 中,
中, , 连接
, 连接 . 设
. 设 , 若正方形
, 若正方形 与正方形
与正方形 的面积之比为
的面积之比为 , 则
, 则 ( )
( )

- A、 5
- B、 4
- C、 3
- D、 2
如图,在 中,以点
中,以点 为圆心,适当长为半径作弧,交
为圆心,适当长为半径作弧,交 于点
于点 , 交
, 交 于点
于点 , 分别以点
, 分别以点 ,
,  为圆心,大于
为圆心,大于 长为半径作弧,两弧在
长为半径作弧,两弧在 的内部交于点
的内部交于点 , 作射线
, 作射线 交
交 于点
于点 . 若
. 若 ,
,  , 则
, 则 的长为( )
的长为( )

- A、
- B、 1
- C、
- D、 2
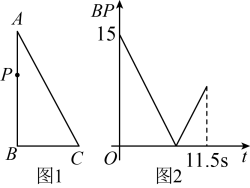
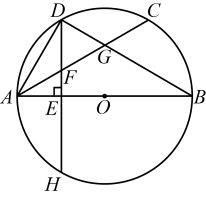
如图,在 中,弦
中,弦 相交于点P,若
相交于点P,若 , 则
, 则 的度数为( )
的度数为( )

- A、
- B、
- C、
- D、
如图,在 中,
中, , 以点A为圆心,以
, 以点A为圆心,以 的长为半径作弧交
的长为半径作弧交 于点D,连接
于点D,连接 , 再分别以点B,D为圆心,大于
, 再分别以点B,D为圆心,大于 的长为半径作弧,两弧交于点P,作射线
的长为半径作弧,两弧交于点P,作射线 交
交 于点E,连接
于点E,连接 , 则下列结论中不正确的是( )
, 则下列结论中不正确的是( )

- A、
- B、
- C、
- D、
下列说法错误的是( )
- A、 成语“水中捞月”表示的事件是不可能事件
- B、 一元二次方程
有两个相等的实数根
- C、 任意多边形的外角和等于
- D、 三角形三条中线的交点叫作三角形的重心
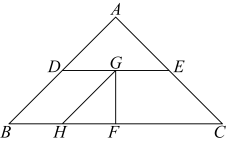
如图, 是等边
是等边 的边
的边 上的高,以点
上的高,以点 为圆心,
为圆心, 长为半径作弧交
长为半径作弧交 的延长线于点
的延长线于点 , 则
, 则 ( )
( )

- A、
- B、
- C、
- D、
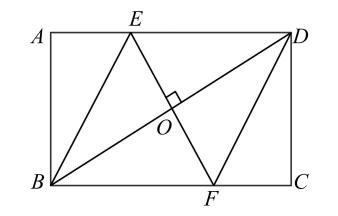
如图,将矩形 对折,使边
对折,使边 与
与 ,
,  与
与 分别重合,展开后得到四边形
分别重合,展开后得到四边形 . 若
. 若 ,
,  , 则四边形
, 则四边形 的面积为( )
的面积为( )

- A、 2
- B、 4
- C、 5
- D、 6