选择题
在平面直角坐标系中,二次函数 的顶点坐标是
的顶点坐标是 ( )
( )
- A、
- B、
- C、
- D、
关于二次函数 的图象,下列说法错误的是( )
的图象,下列说法错误的是( )
- A、 开口向下
- B、 对称轴是直线
- C、 与x轴没有交点
- D、 当
时,y随x的增大而减小
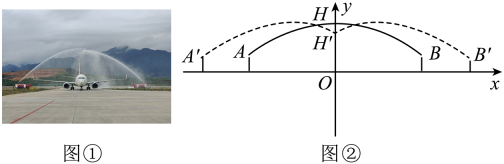
已知实心球运动的高度 与水平距离
与水平距离 之间的函数关系是
之间的函数关系是 , 则该同学此次投掷实心球的成绩是( )
, 则该同学此次投掷实心球的成绩是( )
- A、
- B、
- C、
- D、
关于x的二次函数 在y轴右侧y随x的增大而减小,则a的范围为( )
在y轴右侧y随x的增大而减小,则a的范围为( )
- A、
- B、
- C、
- D、
将抛物线 向上平移3个单位长度得到的抛物线是( )
向上平移3个单位长度得到的抛物线是( )
- A、
- B、
- C、
- D、
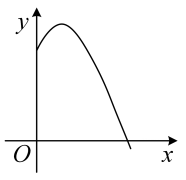
小兰画了一个函数 的图象如图,关于
的图象如图,关于 的方程
的方程 的解是( )
的解是( )

- A、 无解
- B、
- C、
- D、
或