【备考2024】高考数学（函数版块）细点逐一突破训练：对数函数2-组卷题库站

选择题

在北京冬奥会上，国家速滑馆“冰丝带”使用高效环保的二氧化碳跨临界直冷制冰技术，为实现绿色冬奥作出了贡献，如图描述了一定条件下二氧化碳所处的状态与 $\text{[math]}$ 和 $\text{[math]}$ 的关系，其中 $\text{[math]}$ 表示温度，单位是 $\text{[math]}$ ； $\text{[math]}$ 表示压强，单位是bar，下列结论中正确的是（）

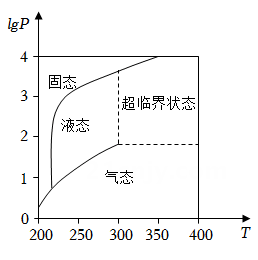
A、当 $\text{[math]}$ ， $\text{[math]}$ 时，二氧化碳处于液态

B、当 $\text{[math]}$ ， $\text{[math]}$ 时，二氧化碳处于气态

C、当 $\text{[math]}$ ， $\text{[math]}$ 时，二氧化碳处于超临界状态

D、当 $\text{[math]}$ ， $\text{[math]}$ 时，二氧化碳处于超临界状态

青少年视力是社会普遍关注的问题，视力情况可借助视力表测量，通常用五分记录法和小数记录法记录视力数据，五分记录法的数据L和小数记数法的数据V满足L=5+lgV。已知某同学视力的五分记录法的数据为4.9，则其视力的小数记数法的数据约为（）（ $\text{[math]}$ ≈1.259）

若 $\text{[math]}$ ，则 $\text{[math]}$ （）

A、 -1

B、 $\text{[math]}$

C、 1

D、 $\text{[math]}$

设a=log₃2，b=log₅3，c= $\text{[math]}$ ，则（）

若 $\text{[math]}$ ，则（）

A、 $\text{[math]}$ 是等差数列

B、 $\text{[math]}$ 是等比数列

C、 $\text{[math]}$ 是等差数列

D、 $\text{[math]}$ 是等比数列

已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，试比较a，b，c的大小关系为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

已知 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

2020年12月17日凌晨1时59分，嫦娥五号返回器携带月球样品成功着陆，这是我国首次实现了地外天体采样返回，标志着中国航天向前又迈出了一大步．月球距离地球约38万千米，有人说：在理想状态下，若将一张厚度约为0.1毫米的纸对折 $\text{[math]}$ 次其厚度就可以超过到达月球的距离，那么至少对折的次数 $\text{[math]}$ 是（）（ $\text{[math]}$ ， $\text{[math]}$ ）

溶液酸碱度是通过 $\text{[math]}$ 计量的， $\text{[math]}$ 的计算公式为 $\text{[math]}$ ，其中 $\text{[math]}$ 表示溶液中氢离子的浓度，单位是摩尔/升．已知某溶液的 $\text{[math]}$ 值为2.921，则该溶液中氢离子的浓度约为（）（取 $\text{[math]}$ ， $\text{[math]}$ ）

A、 $\text{[math]}$ 摩尔/升

B、 $\text{[math]}$ 摩尔/升

C、 $\text{[math]}$ 摩尔/升

D、 $\text{[math]}$ 摩尔/升

若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则关于a、b、c的大小关系，下列说法正确的是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

香农-威纳指数（ $\text{[math]}$ ）是生态学中衡量群落中生物多样性的一个指数，其计算公式是 $\text{[math]}$ ，其中 $\text{[math]}$ 是该群落中生物的种数， $\text{[math]}$ 为第 $\text{[math]}$ 个物种在群落中的比例，下表为某个只有甲､乙､丙三个种群的群落中各种群个体数量统计表，根据表中数据，该群落的香农-威纳指数值为（）

物种	甲	乙	丙	合计
个体数量	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

已知数列 $\text{[math]}$ 是首项为 $\text{[math]}$ 的正项等比数列，若A，B，C是直线l上不同的三点，O为平面内任意一点，且 $\text{[math]}$ ，则（）

已知 $\text{[math]}$ ，且 $\text{[math]}$ ，则下列不等关系成立的是（）

已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则下列判断正确的是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

填空题

计算： $\text{[math]}$ ．

已知函数 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，使得 $\text{[math]}$ ，则 $\text{[math]}$ ．

已知函数 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

$\text{[math]}$ ．

某牧场2022年年初牛的存栏数为1200，计划以后每年存栏数的增长率为20%，且在每年年底卖出100头牛，按照该计划预计年初的存栏量首次超过8900头.（参考数据： $\text{[math]}$ ， $\text{[math]}$ ）

某射手每次射击击中目标的概率均为0.6，该名射手至少需要射击次才能使目标被击中的概率超过0.999，（参考数据： $\text{[math]}$ ， $\text{[math]}$ ）

在如今这个5G时代，6G研究己方兴末艾，2021年8月30日第九届未来信息通信技术国际研讨会在北京举办，会上传出消息，未来6G速率有望达到1Tbps，并启用毫米波、太赫兹、可见光等尖端科技，有望打造出空天地融合的立体网络，预计6G数据传输速率有望比5G快100倍，时延达到亚毫秒级水平．香农公式 $\text{[math]}$ 是被广泛公认的通信理论基础和研究依据，它表示：在受噪声干扰的信道中，最大信息传递率 $\text{[math]}$ 取决于信道宽带 $\text{[math]}$ ，信道内信号的平均功率 $\text{[math]}$ ，信道内部的高斯噪声功率 $\text{[math]}$ 的大小，其中 $\text{[math]}$ 叫做信噪比．若不改变宽带 $\text{[math]}$ ，而将信噪比 $\text{[math]}$ 从11提升至499，则最大信息传递率 $\text{[math]}$ 会提升到原来的倍．（结果保留一位小数）

计算： $\text{[math]}$ .

生物入侵是指生物由原生存地侵入到另一个新的环境，从而对入侵地的生态系统造成危害的现象.若某入侵物种的个体平均繁殖数量为 $\text{[math]}$ ，一年四季均可繁殖，繁殖间隔T为相邻两代间繁殖所需的平均时间.在物种入侵初期，可用对数模型 $\text{[math]}$ （ $\text{[math]}$ 为常数）来描述该物种累计繁殖数量 $\text{[math]}$ 与入侵时间K（单位：天）之间的对应关系，且 $\text{[math]}$ ，在物种入侵初期，基于现有数据得出 $\text{[math]}$ ， $\text{[math]}$ .据此估计该物种累计繁殖数量比初始累计繁殖数量增加 $\text{[math]}$ 倍所需要的时间为（ $\text{[math]}$ ， $\text{[math]}$ ）天.

实数 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为.

解答题

已知函数 $\text{[math]}$ 和 $\text{[math]}$ 有相同的最小值.

已知各项均为正数的等差数列 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等比数列.

已知数列 $\text{[math]}$ 是首项为4，公差为2的等差数列.( $\text{[math]}$ 为常数， $\text{[math]}$ 且 $\text{[math]}$ ).

(Ⅰ)求证：数列 $\text{[math]}$ 是等比数列；

(Ⅱ)当 $\text{[math]}$ 时，设 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ .

设数列 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ ， $\text{[math]}$ .

已知函数 $\text{[math]}$ ，求证：

已知函数 $\text{[math]}$ ．

已知函数 $\text{[math]}$ 的图象在点 $\text{[math]}$ 处的切线方程为 $\text{[math]}$ ．

已知函数 $\text{[math]}$ （ $\text{[math]}$ ，且a为常数）．

某公司欲投资一新型产品的批量生产，预计该产品的每日生产总成本价格)y(单位：万元)是每日产量x(单位：吨)的函数： $\text{[math]}$ .

已知数列 $\text{[math]}$ 是公比为正数的等比数列，其前 $\text{[math]}$ 项和为 $\text{[math]}$ ，满足 $\text{[math]}$ ，且 $\text{[math]}$ 成等差数列.

已知等比数列{a_n}（其中n∈N^*），前n项和记为S_n ，满足： $\text{[math]}$ ，

log₂a_n+1＝﹣1+log₂a_n ．