选择题(每题3分,共30分)
下列各图形中,经过折叠能围成一个立方体的为( )
- A、

- B、

- C、
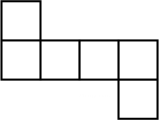
- D、
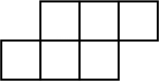
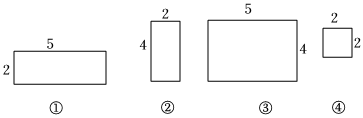
下面图形中,是直棱柱的表面展开图的是( )
- A、

- B、

- C、

- D、

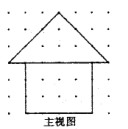
如图所示,该正方体的展开图为( )

- A、

- B、

- C、

- D、

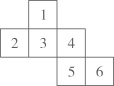
如图是每个面都标注了字母的立方体表面展开图.在展开前,与标注字母  的面相对的面上的字母为( )
的面相对的面上的字母为( )

- A、
- B、
- C、
- D、
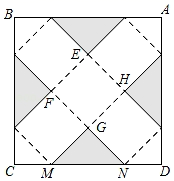
已知图1的小正方形和图2中所有的小正方形都全等,将图1的小正方形安放在图2中的①、②、③、④的其中某一个位置,放置后所组成的图形是不能围成一个正方体的.那么安放的位置是( )

- A、 ①
- B、 ②
- C、 ③
- D、 ④
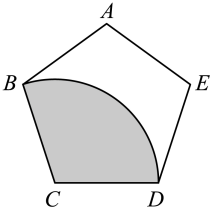
如图,从一个边长是10的正五边形纸片上剪出一个扇形(阴影部分),将剪下来的扇形围成一个圆锥,这个圆锥的底面半径为( )
- A、 1
- B、 3
- C、
- D、 2
如图,在四边形ABCD中,BC=CD=4,AB=7,AB⊥BC,CD⊥BC。把四边形ABCD绕AB旋转一周,则该几何体的表面积为( )

- A、 48π
- B、 56π
- C、 68π
- D、 72π
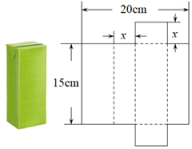
如图1所示,一只封闭的圆柱形容器内盛了一半水(容器的厚度忽略不计),圆柱形容器底面直径为高的2倍,现将该容器竖起后如图2所示,设图1、图2中水所形成的几何体的表面积分别为S1、S2 , 则S1与S2的大小关系是( )

- A、 S1≤S2
- B、 S1<S2
- C、 S1>S2
- D、 S1=S2