选择题
如图,AB=4,以O为圆心,AB为直径作半圆,点C是半圆一动点,若BC=2BD,∠CBD=60°,则线段AD的最大值为( )
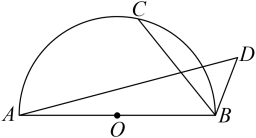
- A、 2
+2
- B、
+1
- C、 3
- D、 2
+1
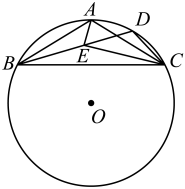
如图,已知点 均在
均在 上,
上, 为
为 的直径,弦
的直径,弦 的延长线与弦
的延长线与弦 的延长线交于点
的延长线交于点 , 连接
, 连接 . 则下列命题为假命题的是( )
. 则下列命题为假命题的是( )
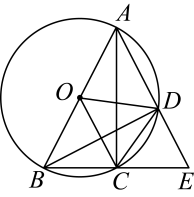
- A、 若点
是
的中点,则
- B、 若
, 则
- C、 若
, 则
- D、 若半径
平分弦
, 则四边形
是平行四边形
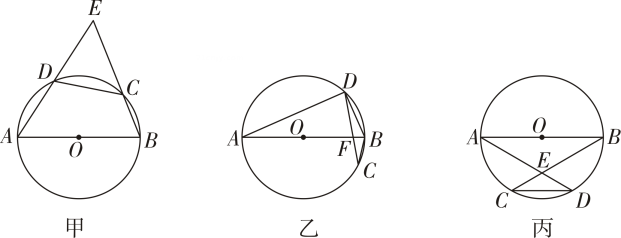
如图,已知点C是线段AB的中点,CD⊥AB且CD= AB=a,延长CB至E,使得BE=b,以CD,CE为边作矩形CEFD,连接并延长DB,交FE的延长线于点G,连接AG,《几何原本》中利用该图解释了代数式(2a+b)2+b2=2[(a+b)2+a2]的几何意义,以AG为直径作圆,交AF于点H,若a=9,b=6,则HG的长为( )
AB=a,延长CB至E,使得BE=b,以CD,CE为边作矩形CEFD,连接并延长DB,交FE的延长线于点G,连接AG,《几何原本》中利用该图解释了代数式(2a+b)2+b2=2[(a+b)2+a2]的几何意义,以AG为直径作圆,交AF于点H,若a=9,b=6,则HG的长为( )

- A、 5
- B、 18
- C、 3
- D、 17
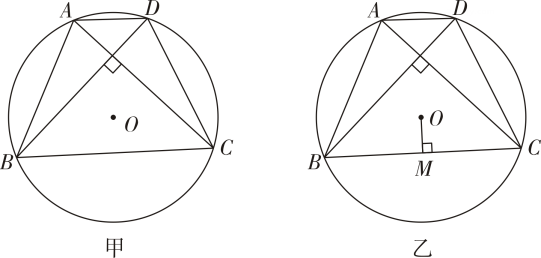
如图,在矩形ABCD中,AB>AD,∠DAB的平分线与CD交于点E,过点C作CF⊥AE于点F,连接BF,DF.有下列结论:①DE=BC;②DF=BF;③∠CDF=∠CBF;④B,C,D,F四点在同一个圆上.其中正确结论的个数为( )

- A、 1
- B、 2
- C、 3
- D、 4
如图,在给定的锐角三角形ABC中,∠BAC=60°,D是边BC上的一个动点,以AD为直径作⊙O分别交边AB,AC于点E,F,连接EF,当点D从点B运动到点C的过程中,线段EF的长度的大小变化情况是( )
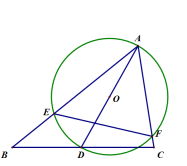
- A、 一直不变
- B、 一直减少
- C、 先减小后增大
- D、 先增大后减小
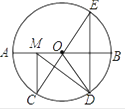
如图,AB是⊙O的直径,点C,点D是半圆上两点,连结AC,BD相交于点P,连结AD,OD.已知OD⊥AC于点E,AB=2.下列结论:
①AD2+AC2=4;②∠DBC+∠ADO=90°;③若AC=BD,则DE=OE;④若点P为BD的中点,则DE=2OE.
其中正确的是( )
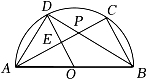
- A、 ①②③
- B、 ②③④
- C、 ③④
- D、 ②④
如图,AB是半圆O的直径,点C、E是半圆上的动点(不与点A、B重合),且 =
= , 射线AE,BC交于点F,M为AF中点,G为CM上一点,作∠GON=
, 射线AE,BC交于点F,M为AF中点,G为CM上一点,作∠GON= , 交BC于点N,则点C在从点A往点B运动的过程中,四边形CGON的面积( )
, 交BC于点N,则点C在从点A往点B运动的过程中,四边形CGON的面积( )
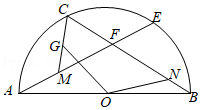
- A、 先变大后变小
- B、 先变小后变大
- C、 保持不变
- D、 一直减小
如图,AB为⊙O的直径,点C为⊙O上一点,连接CO,作AD  OC,若CO=
OC,若CO=  ,AC=2,则AD=( )
,AC=2,则AD=( )
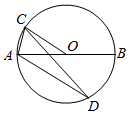
- A、 3
- B、
- C、
- D、
如图,点C是以AB为直径的圆上一个动点(不与点A、B重合),且AC+BC=12.若AB=m(m为整数),则整数m的值的个数为( )
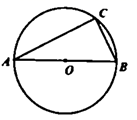
- A、 0个
- B、 2个
- C、 3个
- D、 4个