单选题
如图,直线 被
被 所截,
所截, , 求证:
, 求证: .
.


下列是佳宁同学的证明过程:
证明:
(填依据).
则下列关于上述证明过程中括号内填依据正确的是( )
- A、 两直线平行,同位角相等
- B、 两直线平行,内错角相等
- C、 同位角相等,两直线平行
- D、 内错角相等,两直线平行
老师布置了一项作业,对一个真命题进行证明,下面是小云给出的证明过程:
证明:如图, ,
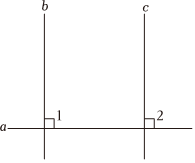
.
,
,
,
.
已知该证明过程是正确的,则证明的真命题是( )
- A、 在同一平面内,若
, 且
, 则
- B、 在同一平面内,若
, 且
, 则
- C、 两直线平行,同位角不相等
- D、 两直线平行,同位角相等
在 和
和 中,
中, ,
,  , 若要证明
, 若要证明 ≌
≌ , 还需要补充一个条件,则正确的补充方法是( )
, 还需要补充一个条件,则正确的补充方法是( )
- A、
- B、
- C、
- D、
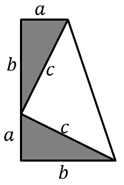
用4个长为 , 宽为
, 宽为 的长方形拼成如图所示的大正方形,则用这个图形可以验证的恒等式是( )
的长方形拼成如图所示的大正方形,则用这个图形可以验证的恒等式是( )

- A、
- B、
- C、
- D、