选择题(本大题共10个小题,每小题4分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
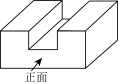
一个几何体如图水平放置,它的俯视图是( )
- A、

- B、

- C、

- D、

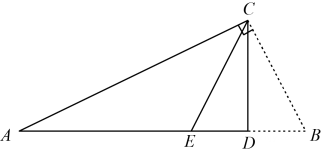
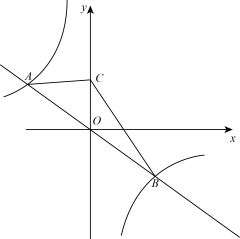
如图,在Rt△ABC中, ,
,  ,
,  , 则∠A的正切值是( )
, 则∠A的正切值是( )

- A、
- B、
- C、
- D、
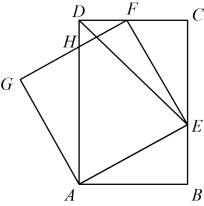
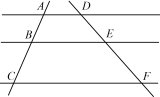
如图,两条直线被三条平行线所截,若 ,
,  , 则EF为( )
, 则EF为( )
- A、 5
- B、 6
- C、 7
- D、 8
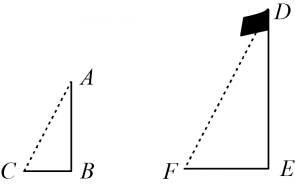
如图,小明同学利用相似三角形测量旗杆的高度,若测得木杆AB长2m,它的影长BC为1m,旗杆DE的影长EF为6m,则旗杆DE的高度为( )
- A、 9m
- B、 10m
- C、 11m
- D、 12m
已知点 ,
,  ,
,  都在反比例函数
都在反比例函数 的图象上,则
的图象上,则 的大小关系为( )
的大小关系为( )
- A、
- B、
- C、
- D、
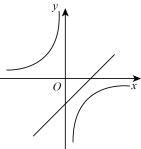
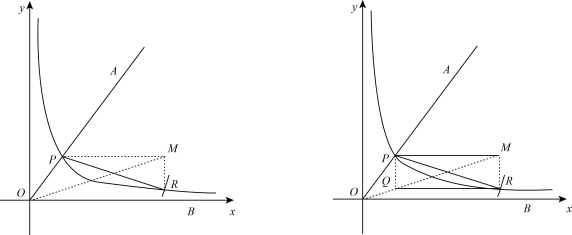
一次函数 与反比例函数
与反比例函数 在同一平面直角坐标系中的图象可能是( )
在同一平面直角坐标系中的图象可能是( )
- A、

- B、

- C、

- D、