选择题
用一个平面去截一个几何体,截面不可能是圆的几何体的是( )
- A、

- B、

- C、
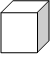
- D、

用平面截一个正方体,可能截出的边数最多的多边形是( )
- A、 七边形
- B、 六边形
- C、 五边形
- D、 四边形
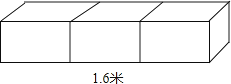
按照图中的方式用一个平面去截长方体,则截面形状是( )

- A、

- B、

- C、

- D、

下面说法,错误的是( )

- A、 一个平面截一个球,得到的截面一定是圆
- B、 一个平面截一个正方体,得到的截面可以是五边形
- C、 棱柱的截面不可能是圆
- D、 甲、乙两图中,只有乙才能折成正方体
下列说法不正确的是( )
- A、 用一个平面去截一个正方体可能截得五边形
- B、 五棱柱有10个顶点
- C、 沿直角三角形某条边所在的直线旋转一周,所得的几何体为圆柱
- D、 将折起的扇子打开,属于“线动成面”的现象
如图,用一个平面从不同的角度去截一个正方体,则截面大小、形状相同的是( )

- A、 ①②相同‘③④相同
- B、 ①③相同;②④相同
- C、 ①④相同;②③相同
- D、 都不相同
如图,正方体的棱长为  cm,用经过A、B、C三点的平面截这个正方体,所得截面的周长是( )
cm,用经过A、B、C三点的平面截这个正方体,所得截面的周长是( )

- A、 2cm
- B、 3
cm
- C、 6cm
- D、 8cm
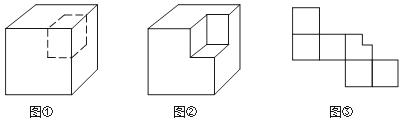
如图是将正方体切去一个角后的几何体,则该几何体有( )

- A、 7个面,14条棱
- B、 6个面,12条棱
- C、 7个面,12条棱
- D、 8个面,13条棱
如图是一个正方体被截去一个正三棱锥得到的几何体,该几何体的俯视图为( )

- A、

- B、

- C、

- D、

图1是一个正六面体,把它按图2中所示方法切割,可以得到一个正六边形的截面,则下列展开图中正确画出所有的切割线的是( )

- A、

- B、

- C、

- D、