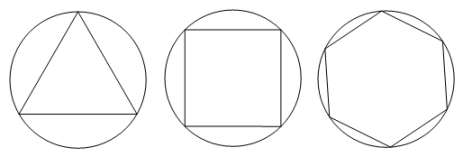
沪科版初中数学九年级下册 24.6.1 正多边形与圆同步分层训练基础卷

日期: 2025-03-29 同步测试来源：出卷网

选择题

一个圆的内接正多边形中，一条边所对的圆心角为72°，则该正多边形的边数是（）

A、 3．

B、 4．

C、 5．

D、 6．

如图，五边形 $\text{[math]}$ 是⊙O的内接正五边形，则 $\text{[math]}$ 的度数为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

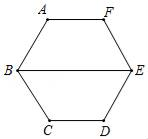
在正六边形ABCDEF的中，若BE=10，则这个正六边形外接圆半径是（）

A、 $\text{[math]}$

B、 5

C、 $\text{[math]}$

D、 5 $\text{[math]}$

已知正六角形的边心距为 $\text{[math]}$ ，则它的周长是（）

A、 6

B、 12

C、 6 $\text{[math]}$

D、 12 $\text{[math]}$

如图，正六边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，若 $\text{[math]}$ 的边心距 $\text{[math]}$ ，则正六边形的边长是（）．

A、 $\text{[math]}$

B、 3

C、 6

D、 $\text{[math]}$

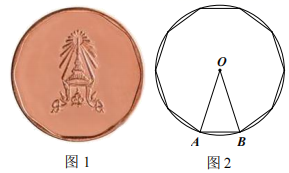
一元钱硬币的直径约为24mm，则用它能完全覆盖住的正六边形的边长最大不超过（）．

A、 12 mm

B、 $\text{[math]}$ mm

C、 6mm

D、 $\text{[math]}$ mm

$\text{[math]}$ 内有一个内接正三角形和一个内接正方形，则内接三角形与内接正方形的边长之比为（）.

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 3：2

D、 1：2

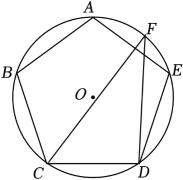
如图，正五边形 $\text{[math]}$ 内接于 $\text{[math]}$ ，点F在弧 $\text{[math]}$ 上.若 $\text{[math]}$ ，则 $\text{[math]}$ 的大小为（）

A、 38°

B、 42°

C、 48°

D、 58°

填空题

已知△ABC的边BC= $\text{[math]}$ ，且△ABC内接于半径为4cm的⊙O ，则∠A的度数为．

如图，正六边形 $\text{[math]}$ 内接于半径为1的 $\text{[math]}$ ，则 $\text{[math]}$ 的长为.

正六边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的半径是 $\text{[math]}$ .

我国魏晋时期的数学家刘徽首创“割圆术”，利用圆的内接正多边形逐步逼近圆来近似计算圆的面积．如图，若用圆的内接正八边形的面积 $\text{[math]}$ 来近似估计 $\text{[math]}$ 的面积 $\text{[math]}$ ，设 $\text{[math]}$ 的半径为2，则 $\text{[math]}$ 的值为．（结果保留和根号）

如图，已知⊙O的半径为2，等边三角形ABC内接于⊙O，则 $\text{[math]}$ 的度数为，△ABC的边长为

解答题

如图，正八边形 $\text{[math]}$ 内接于 $\text{[math]}$ ， M是弧DE上的一点，连接AM ， BM ，求 $\text{[math]}$ 的度数．

小明绘制了如图所示的图形.图中六个形状大小都相同的四边形围成了一个圆的内接正六边形和一个小正六边形.若PQ所在的直线经过点M，PB=5cm，小正六边形的面积为 $\text{[math]}$ ，求该圆的半径.

综合题

如图，正三角形、正方形、正六边形等正n边形与圆的形状有差异，我们将正n边形与圆的接近程度称为“接近度”.

图1是某景区的纪念币，一面有一个正十边形，示意图如图2所示，其外接圆的圆心为O，直径为 $\text{[math]}$ .

相关试卷推荐

友情链接

组卷网课件下载备课易 StirlingPdf 排课软件云字帖

2016-2022 组卷题库
组卷题库试题答案查询