选择题
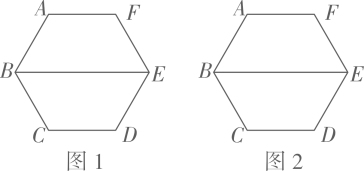
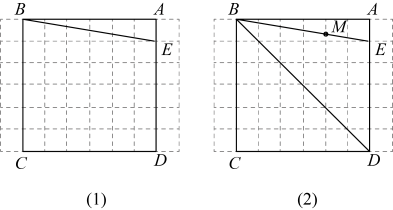
如图,将四根木条用钉子钉成一个矩形框架 , 然后向左扭动框架,观察所得四边形的变化.下面判断错误的是( )
, 然后向左扭动框架,观察所得四边形的变化.下面判断错误的是( )

- A、 四边形
由矩形变为平行四边形
- B、 对角线
的长度减小
- C、 四边形
的面积不变
- D、 四边形
的周长不变
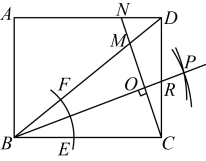
如图,矩形 中,
中, , 以点B为圆心,适当长为半径画弧,分别交
, 以点B为圆心,适当长为半径画弧,分别交 ,
,  于点E,F,再分别以点E,F为圆心,大于
于点E,F,再分别以点E,F为圆心,大于 长为半径画弧交于点P,作射线
长为半径画弧交于点P,作射线 , 过点C作
, 过点C作 的垂线分别交
的垂线分别交 于点M,N,则
于点M,N,则 的长为( )
的长为( )
- A、
- B、
- C、
- D、 4
下列图案中, 是中心对称图形.( )
- A、

- B、

- C、

- D、

如图,有一张矩形纸片 先对折矩形
先对折矩形 , 使
, 使 与
与 重合,得到折痕
重合,得到折痕 , 把纸片展平
, 把纸片展平 再一次折叠纸片,使点
再一次折叠纸片,使点 落在
落在 上,并使折痕经过点
上,并使折痕经过点 , 得到折痕
, 得到折痕 , 同时得到线段
, 同时得到线段 ,
,  观察所得的线段,若
观察所得的线段,若 , 则
, 则 ( )
( )

- A、
- B、
- C、
- D、
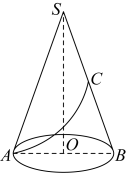
如图,根据三视图,它是由个正方体组合而成的几何体.( )
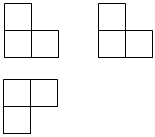
- A、
- B、
- C、
- D、
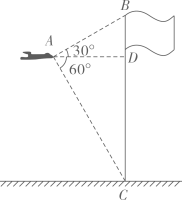
将含 角的直角三角板按如图方式摆放,已知
角的直角三角板按如图方式摆放,已知 ,
,  , 则
, 则 ( )
( )
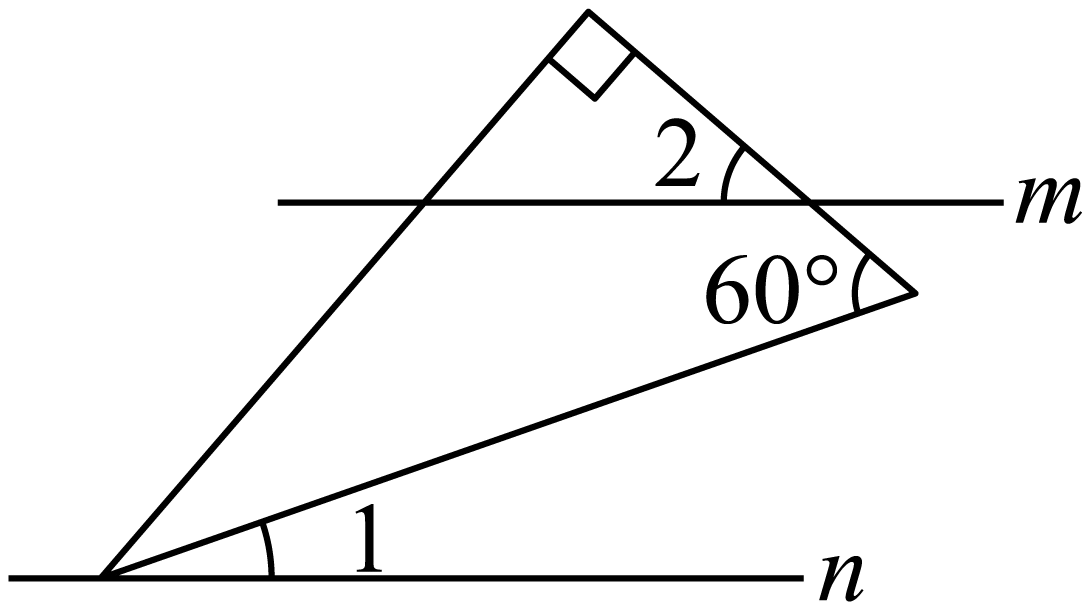
- A、
- B、
- C、
- D、
如图,在 中,
中, 分别交
分别交 于点D , E ,
于点D , E ,  交
交 于点F ,
于点F ,  ,
,  , 则
, 则 的长为( )
的长为( )
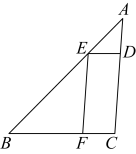
- A、
- B、
- C、 2
- D、 3
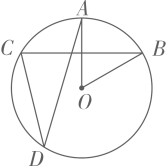
如图,在 中,直径
中,直径 与弦
与弦 相交于点P,连接
相交于点P,连接 , 若
, 若 ,
,  , 则
, 则 ( )
( )

- A、
- B、
- C、
- D、
如图,在平面直角坐标系中,O为原点,OA=OB= , 点C为平面内一动点,BC=
, 点C为平面内一动点,BC= , 连接AC,点M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM取最大值时,点M的坐标是( )
, 连接AC,点M是线段AC上的一点,且满足CM∶MA=1∶2.当线段OM取最大值时,点M的坐标是( )
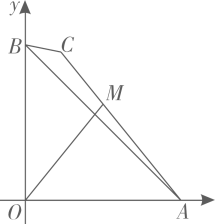
- A、 (
,
)
- B、 (
,
)
- C、 (
,
)
- D、 (
,
)
如图,直线 分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转
分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转 得到△CAD,则点B的对应点D的坐标是( )
得到△CAD,则点B的对应点D的坐标是( )

- A、 (2,5)
- B、 (3,5)
- C、 (5,2)
- D、 (
, 2)
如图,一条公路的转弯处是一段圆弧( ),点O是这段弧所在圆的圆心,B为
),点O是这段弧所在圆的圆心,B为 上一点,OB⊥AC于D. 若AC=
上一点,OB⊥AC于D. 若AC= m,BD=150m,则
m,BD=150m,则 的长为( )
的长为( )

- A、
m
- B、
m
- C、
m
- D、
m
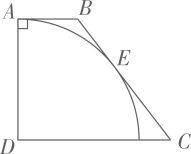
如图,在四边形 中,
中, , 以
, 以 为圆心,
为圆心, 为半径的弧恰好与
为半径的弧恰好与 相切,切点为
相切,切点为 . 若
. 若 , 则
, 则 的值是( )
的值是( )
- A、
- B、
- C、
- D、