2024年人教A版高二下学期数学期中模拟试卷二

日期: 2025-04-13 期中考试来源：出卷网

选择题（每题5分，共40分）

已知 $\text{[math]}$ 为实数，复数 $\text{[math]}$ 为纯虚数，则 $\text{[math]}$ （）

A、 -1

B、 1

C、 -2

D、 2

已知正项等比数列 $\text{[math]}$ ，则 $\text{[math]}$ ，则公比 $\text{[math]}$ 为（）

A、 $\text{[math]}$

B、 2

C、 $\text{[math]}$

D、 4

抛掷一个质地均匀的股子的试验，事件 $\text{[math]}$ 表示“小于5的偶数点出现”，事件 $\text{[math]}$ 表示“不小于5的点数出现”，则一次试验中，事件 $\text{[math]}$ 或事件 $\text{[math]}$ 至少有一个发生的概率为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为不同的平面，m ， n ， l为不同的直线，则下列条件中一定能得到 $\text{[math]}$ 的是（）

A、 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

B、 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

C、 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

D、 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

直线 $\text{[math]}$ 被圆 $\text{[math]}$ 截得的弦长为（）

A、 2

B、 $\text{[math]}$

C、 4

D、 $\text{[math]}$

“方斗”常作为盛米的一种容器，其形状是一个上大下小的正四棱台，现有“方斗”容器如图所示，已知 $\text{[math]}$ ，现往容器里加米，当米的高度是“方斗”高度的一半时，用米 $\text{[math]}$ ，则该“方斗”可盛米的总质量为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

已知函数 $\text{[math]}$ 的导函数 $\text{[math]}$ 的图象如图所示，则下列结论中正确的是（）

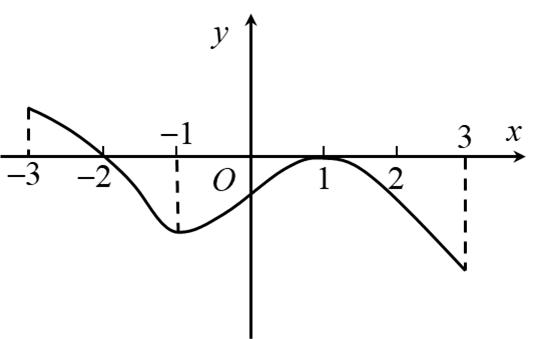
A、曲线 $\text{[math]}$ 在点 $\text{[math]}$ 处的切线斜率小于零

B、函数 $\text{[math]}$ 在区间 $\text{[math]}$ 上单调递增

C、函数 $\text{[math]}$ 在 $\text{[math]}$ 处取得极大值

D、函数 $\text{[math]}$ 在区间 $\text{[math]}$ 内至多有两个零点

已知直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 无公共交点，则 $\text{[math]}$ 的离心率的取值范围是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

多项选择题（每题6分，共18分）

已知一组样本数据 $\text{[math]}$ ，则这组数据的（）

高二年级安排甲、乙、丙三位同学到A ， B ， C ， D ， E五个社区进行暑期社会实践活动，每位同学只能选择一个社区进行活动，且多个同学可以选择同一个社区进行活动，下列说法正确的有（）

在数学中，布劳威尔不动点定理是拓扑学里的一个非常重要的不动点定理，它得名于荷兰数学家鲁伊兹*布劳威尔.简单的讲就是对于满足一定条件的连续函数 $\text{[math]}$ ，存在一个点 $\text{[math]}$ ，使得 $\text{[math]}$ ，那么我们称该函数为“不动点”函数，而称 $\text{[math]}$ 为该函数的一个不动点，依据不动点理论，下列说法正确的是（）

填空题（每题5分，共15分）

若 $\text{[math]}$ ，则 $\text{[math]}$ ．

设 $\text{[math]}$ ， $\text{[math]}$ 是不共线的向量，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， A ， B ， D三点共线，则 $\text{[math]}$ 的值为.

若函数 $\text{[math]}$ 有两个零点，则正整数 $\text{[math]}$ 的最小值为．（其中 $\text{[math]}$ 是自然对数的底数，参考数据： $\text{[math]}$ ， $\text{[math]}$ ）

解答题（共5题，共77分）

在 $\text{[math]}$ 中，角A，B，C的对边分别为a，b，c，已知 $\text{[math]}$ ．

如图所示，在三棱锥 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．

记 $\text{[math]}$ 为等比数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和.已知 $\text{[math]}$ .

动点P与定点 $\text{[math]}$ 的距离和它到直线 $\text{[math]}$ 的距离的比是常数 $\text{[math]}$ ，记点P的轨迹为E.

在几何学常常需要考虑曲线的弯曲程度，为此我们需要刻画曲线的弯曲程度．考察如图所示的光滑曲线C： $\text{[math]}$ 上的曲线段 $\text{[math]}$ ，其弧长为 $\text{[math]}$ ，当动点从A沿曲线段 $\text{[math]}$ 运动到B点时，A点的切线 $\text{[math]}$ 也随着转动到B点的切线 $\text{[math]}$ ，记这两条切线之间的夹角为 $\text{[math]}$ （它等于 $\text{[math]}$ 的倾斜角与 $\text{[math]}$ 的倾斜角之差）．显然，当弧长固定时，夹角越大，曲线的弯曲程度就越大；当夹角固定时，弧长越小则弯曲程度越大，因此可以定义 $\text{[math]}$ 为曲线段 $\text{[math]}$ 的平均曲率；显然当B越接近A ，即 $\text{[math]}$ 越小，K就越能精确刻画曲线C在点A处的弯曲程度，因此定义 $\text{[math]}$ （若极限存在）为曲线C在点A处的曲率．（其中y＇，y＇＇分别表示 $\text{[math]}$ 在点A处的一阶、二阶导数）

相关试卷推荐

友情链接

组卷网课件下载备课易 StirlingPdf 排课软件云字帖课堂游戏

2016-2025 组卷题库
组卷题库试题答案查询