选择题
等腰三角形中一个外角等于100°,则另两个内角的度数分别为( )
- A、 40°,40°
- B、 80°,20°
- C、 50°,50°
- D、 50°,50°或80°,20°
等腰三角形一腰上的高与另一腰的夹角是50°,则这个等腰三角形的底角为( )
- A、 70°
- B、 20°
- C、 70°或20°
- D、 40°或140°
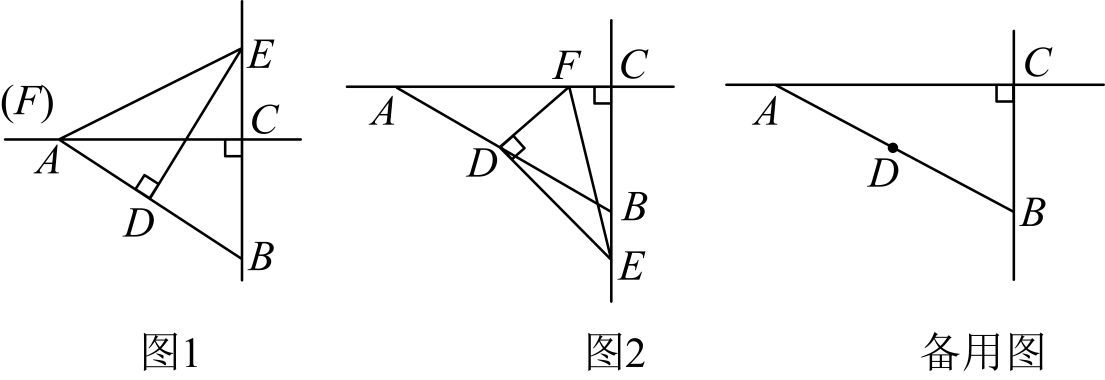
在 中,
中, ,
,  平分
平分 交
交 于点E , 若点E分
于点E , 若点E分 为
为 两部分,则
两部分,则 的长为( )
的长为( )
- A、 1
- B、 1或9
- C、 4
- D、 4或12
若关于x的分式方程 有增根,则m的值为( )
有增根,则m的值为( )
- A、 1.5
- B、 -6
- C、 1或-2
- D、 1.5或-6
等腰三角形的一条边长为4,另一条边长为7,则该三角形的周长为( )
- A、 15
- B、 18
- C、 15或18
- D、 18或23
若等腰三角形的一个外角度数为100°,则该等腰三角形顶角的度数为( )
- A、 80°
- B、 100°
- C、 20°或100°
- D、 20°或80°
若关于x的方程 无解,则m的值为( )
无解,则m的值为( )
- A、 1
- B、 1或3
- C、 1或2
- D、 2或3
在矩形 中,点
中,点 是对角线
是对角线 上一点,
上一点, ,
,  , 当
, 当 为等腰三角形时,
为等腰三角形时, 的长为( )
的长为( )
- A、 1
- B、 2.5
- C、 1.5或2
- D、 1或2.5
在平行四边形ABCD中有一个内角为50°,则∠A的度数为( )
- A、 50°
- B、 100°
- C、 50°或100°
- D、 50°或130°
若关于x的分式方程 有增根,则m的值为( )
有增根,则m的值为( )
- A、 1
- B、 -2
- C、 1或
- D、
或2