新人教版（2024版）七年级上学期数学课时进阶测试5.1从算式到方程（三阶）

日期: 2025-03-28 同步测试来源：出卷网

选择题

下列各等式的变形错误的是（）

A、如果 $\text{[math]}$ ，那么 $\text{[math]}$

B、如果 $\text{[math]}$ ，那么 $\text{[math]}$

C、如果 $\text{[math]}$ ，那么 $\text{[math]}$

D、如果 $\text{[math]}$ ，那么 $\text{[math]}$

已知 $\text{[math]}$ ， $\text{[math]}$ 为有理数，且 $\text{[math]}$ ，若关于 $\text{[math]}$ 的一元一次方程 $\text{[math]}$ 的解恰为 $\text{[math]}$ ，则此方程称为“合并式方程”．例如： $\text{[math]}$ ， ∵ $\text{[math]}$ ，且 $\text{[math]}$ 是方程 $\text{[math]}$ 的解，∴此方程 $\text{[math]}$ 为“合并式方程”．若关于 $\text{[math]}$ 的一元一次方程 $\text{[math]}$ 是“合并式方程”，则 $\text{[math]}$ 的值为（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

如图，已知相同物体的质量相等，①中天平保持平衡状态，则②中天平（）

A、能平衡

B、不能平衡，右边比左边低

C、不能平衡，左边比右边低

D、无法确定

若 $\text{[math]}$ 是关于x的一元一次方程 $\text{[math]}$ 的解，则代数式 $\text{[math]}$ 的值为（）

A、 8

B、 6

C、 4

D、 2

程大位是我国明朝商人，珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著，详述了传统的珠算规则，确立了算盘用法.书中有如下问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁.意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，大、小和尚各有多少人?若设大和尚有x人，则列出的方程正确的是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

对于任意两个实数 $\text{[math]}$ ， $\text{[math]}$ 给出以下两个运算法则：① $\text{[math]}$ ；② $\text{[math]}$ ，例如 $\text{[math]}$ ， $\text{[math]}$ ．解决下列问题：已知正整数 $\text{[math]}$ 满足 $\text{[math]}$ ，且 $\text{[math]}$ ，关于这个四元方程下列说法：① $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是该四元方程的一组解；②连续的四个偶数一定是该四元方程的解；③若 $\text{[math]}$ ，则该四元方程有7组解；正确的个数是（）

A、 0

B、 1

C、 2

D、 3

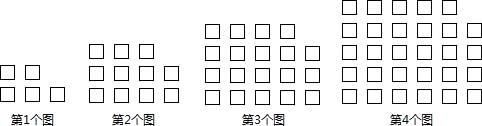
根据图中给出的信息，可得正确的方程是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

洛书是一个三阶幻方，就是将已知的9个数填入 $\text{[math]}$ 的方格中，使每一横行、每一竖列以及两条斜对角线上的数字之和都相等．图1是我国古代传说中的洛书，图2是洛书的数字表示，图3是一个不完整的幻方，根据幻方的规则，由已知数求出 $\text{[math]}$ 的值应为（）

A、 $\text{[math]}$

B、 3

C、 $\text{[math]}$

D、 2

填空题

如图，用相同的小正方形按照某种规律进行摆放，则第6个图形中小正方形的个数是，第n（n为正整数）个图形中小正方形的个数是（用含n的代数式表示）．

如图，将9个数放入“ $\text{[math]}$ ”内，分别记作 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若每条边上3个“ $\text{[math]}$ ”内数字之和相等，即 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 四个数之间的数量关系是； $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三个数之间的数量关系是．

今有共买物，人出八，盈三；人出七，不足四.问人数、物价各几何？意思是：几个人一起去买某物品，如果每人出8钱，则多了3钱；如果每人出7钱，则少了4钱.问有多少人，物品的价格是多少？设有x人，则根据题意列出方程.

如果 $\text{[math]}$ 是关于x的方程 $\text{[math]}$ 的解，那么 $\text{[math]}$ ．

各代表一个数，根据

$\text{[math]}$

$\text{[math]}$ ，

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$ ，求得

$\text{[math]}$

解答题

已知5x²﹣5x﹣3=7，利用等式的性质，求x²﹣x的值．

根据下列各题的条件，写出仍能成立的等式．

相关试卷推荐

友情链接

组卷网课件下载备课易 StirlingPdf 排课软件云字帖

2016-2022 组卷题库
组卷题库试题答案查询