请认真阅读下列材料：

如图①，给定一个以点O为圆心，r为半径的圆，设点A是不同于点O的任意一点，则点A的反演点定义为射线 上一点 ，满足 .

显然点A也是点 的反演点.即点A与点 互为反演点，点O为反演中心，r称为反演半径.这种从点A到点 的变换或从点 到点A的变换称为反演变换.

例如：如图②，在平面直角坐标系中，点 ，以点O为圆心， 为半径的圆，交y轴的正半轴于点B；C为线段 的中点，P是 上任意一点，点D的坐标为 ；若C关于 的反演点分别为 .

（ 1 ）求点 的坐标；

（ 2 ）连接 、 ，求 的最小值.

解：（ 1 ）由反演变换的定义知： ，其中 ， .

∴ ，故点 的坐标为 ；

（ 2 ）如图③，连接 、 ，由反演变换知 ，

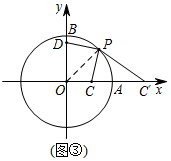
即 ，而 ，

∴ .

∴ ，即 .

∴ .

故 的最小值为13.

请根据上面的阅读材料，解决下列问题：

如图④，在平面直角坐标系中，点 ，以点O为圆心， 为半径画圆，交y轴的正半轴于点B，C为线段 的中点，P是 上任意一点，点D的坐标为 .