试题详情
“垛积术”在我国古代早期主要用于天文历法,后来用于求高阶等差级数的和.元代数学家朱世杰在沈括(北宋时期数学家)、杨辉(南宋时期数学家)研究成果的基础上,在《四元玉鉴》中利用了“三角垛”求一系列重要的高阶等差级数的和.例如,欲求数列  ,
,  ,
,  ,…,
,…,  ,
,  的和,可设计一个正立的
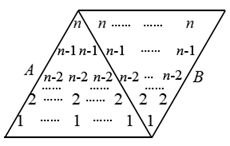
的和,可设计一个正立的  行三角数阵,即正三角形
行三角数阵,即正三角形  的区域中所有数的分布规律为:第1行为1个
的区域中所有数的分布规律为:第1行为1个  ,第2行为2个
,第2行为2个  ,第3行为3个
,第3行为3个  ,…,第
,…,第  行为
行为  个1;再选一个数列
个1;再选一个数列  (其前
(其前  项和已知),可设计一个倒立的
项和已知),可设计一个倒立的  行三角数阵,即正三角形
行三角数阵,即正三角形  的区域中所有数的分布规律为:第1行为
的区域中所有数的分布规律为:第1行为  个
个  ,第2行为
,第2行为  个
个  ,第3行为
,第3行为  个
个  ,…,第
,…,第  行为1个1.这两个三角数阵就组成一个
行为1个1.这两个三角数阵就组成一个  行
行  列的菱形数阵.若已知
列的菱形数阵.若已知  ,则运用垛积术,求得数列
,则运用垛积术,求得数列  ,
,  ,
,  ,…,
,…,  ,
,  的和为.
的和为.