试题详情
完成下面的证明.
如图,已知AD⊥BC,EF⊥BC,∠1=∠2,求证:∠BAC+∠AGD=180°.
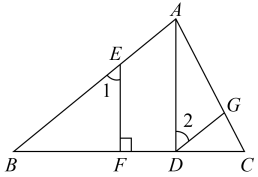
证明:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=90°,∠ADB=90°( ),
∴∠EFB=∠ADB(等量代换),
∴EF//AD( ),
∴∠1=∠BAD( ),
又∵∠1=∠2(已知),
∴∠2=∠ ▲ (等量代换),
∴DG//BA( ),
∴∠BAC+∠AGD=180°( ).
知识点

参考答案
采纳过本试题的试卷
如图,已知AD⊥BC,EF⊥BC,∠1=∠2,求证:∠BAC+∠AGD=180°.

证明:∵AD⊥BC,EF⊥BC(已知),
∴∠EFB=90°,∠ADB=90°( ),
∴∠EFB=∠ADB(等量代换),
∴EF//AD( ),
∴∠1=∠BAD( ),
又∵∠1=∠2(已知),
∴∠2=∠ ▲ (等量代换),
∴DG//BA( ),
∴∠BAC+∠AGD=180°( ).
