填空：把下面的推理过程补充完整，并在括号内注明理由．

已知：如图，△ABC中，D、E分别为AB、AC的中点，过点C作CF∥AB交DE的延长线于F，求证：AB＝2CF ．

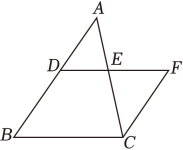
证明：∵CF∥AB（          ），

∴∠ADE＝∠F（          ），

∵E为AC的中点（已知），

∴AE＝CE（          ），

在△ADE与△CFE中，

∠ADE＝∠F ，         ＝         ， AE＝CD ，

∴△ADE≌△CFE（          ），

∴AD＝CF（          ），

∵D为AB的中点，

∴AB＝2AD（中点的定义），

∴AB＝2CF（          ）．