试题详情
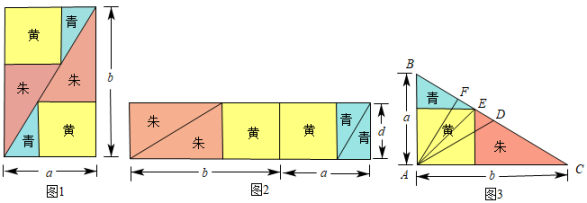
《九章算术》中“勾股容方”问题:“今有勾五步,股十二步,问勾中容方几何?”魏晋时期数学家刘徽在其《九章算术注》中利用出入相补原理给出了这个问题的一般解法:如图1,用对角线将长和宽分别为 和
和 的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形,该矩形长为
的矩形分成两个直角三角形,每个直角三角形再分成一个内接正方形(黄)和两个小直角三角形(朱、青).将三种颜色的图形进行重组,得到如图2所示的矩形,该矩形长为 , 宽为内接正方形的边长
, 宽为内接正方形的边长 .由刘徽构造的图形可以得到许多重要的结论,如图3.设
.由刘徽构造的图形可以得到许多重要的结论,如图3.设 为斜边
为斜边 的中点,作直角三角形
的中点,作直角三角形 的内接正方形对角线
的内接正方形对角线 , 过点
, 过点 作
作 于点
于点 , 则下列推理正确的是( )
, 则下列推理正确的是( )
①由图1和图2面积相等得;
②由可得
;
③由可得
;
④由可得
.
知识点

参考答案
采纳过本试题的试卷