单选题
已知集合  ,
,  ,则
,则  ( )
( )
- A、
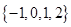
- B、
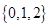
- C、
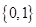
- D、

已知  为虚数单位,复数
为虚数单位,复数  满足
满足  ,则复数
,则复数  的虚部为( )
的虚部为( )
- A、

- B、
- C、

- D、
甲乙两名同学6次考试的成绩统计如下图,甲乙两组数据的平均数分别为  、
、  ,标准差分别为
,标准差分别为  ,则( )
,则( )

- A、
 ,
, 
- B、
 ,
, 
- C、
 ,
, 
- D、
 ,
, 
已知直线  和平面
和平面  ,若
,若  ,则“
,则“  ”是“
”是“  ”的( )
”的( )
- A、 充分不必要条件
- B、 必要不充分条件
- C、 充要条件
- D、 既不充分也不必要条件
已知椭圆  ,则下列结论正确的是( )
,则下列结论正确的是( )
- A、 长轴长为
- B、 焦距为
- C、 短轴长为
- D、 离心率为
执行下面的程序框图,则输出  的值为( )
的值为( )

- A、 99
- B、 98
- C、 100
- D、 101
若在  关于
关于  的展开式中,常数项为2,则
的展开式中,常数项为2,则  的系数是( )
的系数是( )
- A、 60
- B、 45
- C、 42
- D、 -42
已知数列  是等比数列,若
是等比数列,若  ,
,  ,则
,则  ( )
( )
- A、

- B、

- C、

- D、

已知函数  图象相邻两条对称轴之间的距离为
图象相邻两条对称轴之间的距离为  ,将函数
,将函数  的图象向左平移
的图象向左平移  个单位,得到的图象关于
个单位,得到的图象关于  轴对称,则( )
轴对称,则( )
- A、 函数
的周期为

- B、 函数
图象关于点
 对称
对称 - C、 函数
图象关于直线
 对称
对称 - D、 函数
在
 上单调
上单调




