广西柳州2018-2019学年高二下学期理数第一次月考模拟卷

作者UID:10385933

日期: 2024-11-26

月考试卷

单选题

已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

设复数 $\text{[math]}$ ，则 $\text{[math]}$ 的共轭复数是（　　）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

设向量 $\text{[math]}$ ，若t是实数，则 $\text{[math]}$ 的最小值为( )

A、 $\text{[math]}$

B、 $\text{[math]}$

D、 $\text{[math]}$

如图所示，一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的全面积为（　　）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

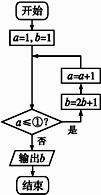
执行如图所示的程序框图，若输出b的值为31，则图中判断框内①处应填( )

设等比数列 $\text{[math]}$ 的公比为_q ，前n项和为 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 成等差数列，则公比q为( ).

B、 q=-2　　　　

C、 q=-2或q=1

D、 q=2或q=-1

已知函数f（x）=2sin²（ $\text{[math]}$ +x）﹣ $\text{[math]}$ cos2x﹣1，x∈R，若函数k（x）=f（x+a）的图象关于点（﹣ $\text{[math]}$ ，0）对称，且α∈（0，π），则α=（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

过抛物线 $\text{[math]}$ 的焦点 $\text{[math]}$ 且斜率为1的直线交抛物线于 $\text{[math]}$ 两点， $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

B、 $\text{[math]}$

$\text{[math]}$ 展开式中 $\text{[math]}$ 的系数为（）

已知函数 $\text{[math]}$ ，若在 $\text{[math]}$ 上任取一个实数 $\text{[math]}$ ，则不等式 $\text{[math]}$ 成立的概率是（）

A、 $\text{[math]}$

B、 $\text{[math]}$

C、 $\text{[math]}$

D、 $\text{[math]}$

已知双曲线的左、右焦点分别为F₁ ， F₂ ，在左支上过F₁的弦AB的长为5，若实轴长度为8，则△ABF₂的周长是（）

命题p：对 $\text{[math]}$ ，都有 $\text{[math]}$ 成立，则P的否定形式为（）

A、对 $\text{[math]}$ ，都有 $\text{[math]}$

B、 $\text{[math]}$ ，都有 $\text{[math]}$

C、 $\text{[math]}$ ，都有 $\text{[math]}$

D、对 $\text{[math]}$ ，都有 $\text{[math]}$

填空题

已知sinα﹣cosα= $\text{[math]}$ ， α∈（0，π），tanα=

设实数x，y满足 $\text{[math]}$ ，则μ= $\text{[math]}$ 的取值范围是．

已知数列{a_n}是公差为d的等差数列，且a₁+a₃+a₅=105，a₂+a₄+a₆=99，则d=，当数列{a_n}的前n项和S_n取得最大值时，n=．

在底面半径为R，高为h的圆锥内有一内接圆柱，则内接圆柱的圆柱的高为时，其侧面积最大值为．

解答题

已知函数f（x）=sin（3x+ $\text{[math]}$ ）．

某市为了了解高二学生物理学习情况，在34所高中里选出5所学校，随机抽取了近千名学生参加物理考试，将所得数据整理后，绘制出频率分布直方图如图所示．

如图所示，已知长方体ABCD﹣A₁B₁C₁D₁中，AB=BC=2，AA₁=4，E是棱CC₁上的点，且BE⊥B₁C．

已知椭圆 $\text{[math]}$ （ $\text{[math]}$ ）的离心率为 $\text{[math]}$ ，点 $\text{[math]}$ 在椭圆上.

（Ⅰ）求椭圆 $\text{[math]}$ 的方程；

（Ⅱ）设 $\text{[math]}$ 是椭圆的一条弦，斜率为 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 轴上的一点， $\text{[math]}$ 的重心为 $\text{[math]}$ ，若直线 $\text{[math]}$ 的斜率存在，记为 $\text{[math]}$ ，问： $\text{[math]}$ 为何值时， $\text{[math]}$ 为定值？

已知函数f（x）=alnx﹣ax﹣3（a≠0）．

已知圆心在原点的圆被直线 $\text{[math]}$ 截得的弦长为 $\text{[math]}$

(Ⅰ)求圆的方程；

(Ⅱ)设动直线 $\text{[math]}$ 与圆 $\text{[math]}$ 交于 $\text{[math]}$ 两点，问在 $\text{[math]}$ 轴正半轴上是否存在定点 $\text{[math]}$ ，使得直线 $\text{[math]}$ 与直线 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称？若存在，请求出点 $\text{[math]}$ 的坐标；若不存在，请说明理由；

已知定义在 $\text{[math]}$ 上的函数 $\text{[math]}$ ， $\text{[math]}$ ，若存在实数 $\text{[math]}$ 使得 $\text{[math]}$ 成立．

试卷列表

教育网站链接

在线组卷课件下载评课网课件工坊 PPT模板排课软件云字帖