选择题
如图，∠1和∠2是对顶角的是（ ）
- A、
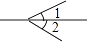
- B、
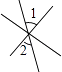
- C、
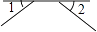
- D、
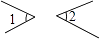
如图，∠1与∠2不是同旁内角的是（ ）
- A、
- B、
- C、
- D、
在实数：3.14159， 
，1.010010001…， 
，4. 
， 
， 
中，无理数有（ ）
- A、 1个
- B、 2个
- C、 3个
- D、 4个
下列运算中，正确的是（ ）
- A、
=±3
- B、
=2
- C、
- D、
如图所示，点E在AC的延长线上，下列条件中能判断AB∥CD的是（ ）
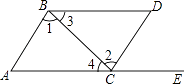
- A、 ∠3=∠4
- B、 ∠1=∠2
- C、 ∠D=∠DCE
- D、 ∠D+∠ACD=180°
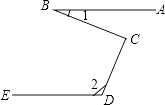
车库的电动门栏杆如图所示，BA垂直于地面AE于A，CD平行于地面AE，则∠ABC+∠BCD的大小是（ ）
- A、 150°
- B、 180°
- C、 270°
- D、 360°
如图，将△ABC沿BC方向平移1个单位得到△DEF，若△ABC的周长等于8，则四边形ABFD的周长等于（ ）
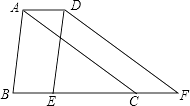
- A、 8
- B、 10
- C、 12
- D、 14
已知点P（2﹣4m，m﹣4）在第三象限，且满足横、纵坐标均为整数的点P有（ ）
- A、 1个
- B、 2个
- C、 3个
- D、 4个
点A（﹣3，﹣5）向上平移4个单位，再向左平移3个单位到点B，则点B的坐标为（ ）
- A、 （1，﹣8）
- B、 （1，﹣2）
- C、 （﹣6，﹣1）
- D、 （0，﹣1）
通过估算，估计 
的大小应在（ ）
- A、 7～8之间
- B、 8.0～8.5之间
- C、 8.5～9.0之间
- D、 9～10之间
下列命题中，正确的是（ ）
- A、 相等的角是对顶角
- B、 两条不相交的线段是平行的
- C、 过一点有且只有一条直线与已知直线平行
- D、 互为邻补角的两角的角平分线互相垂直
点P位于第一象限，距y轴3个单位长度，距离x轴4个单位长度，则点P坐标是（ ）
- A、 （﹣3，4）
- B、 （3，4）
- C、 （﹣4，3）
- D、 （4，3）
如图，数轴上，AB=AC，A，B两点对应的实数分别是 
和﹣1，则点C所对应的实数是（ ）
- A、 1+
- B、 2+
- C、 2
- D、 2
已知点A（1，0），B（0，2），点P在x轴上，且△PAB的面积为5，则点P的坐标是（ ）
- A、 （﹣4，0）
- B、 （6，0）
- C、 （﹣4，0）或（6，0）
- D、 （0，12）或（0，﹣8）
