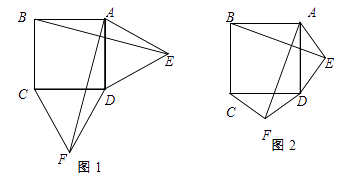
单选题
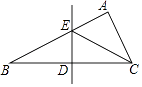
如图所示,BD是△ABC的角平分线,DE垂直平分BC,若∠A=120°,则∠C的度数为( )

- A、 15°
- B、 20°
- C、 25°
- D、 30°
如图,DE为△ABC的边BC的垂直平分线,交BC于E,交AB于D,且∠B=40°,∠A=60°,则∠ACD的度数为( )
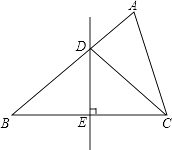
- A、 40°
- B、 50°
- C、 30°
- D、 45°
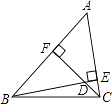
如图,锐角三角形ABC中,直线l为BC的中垂线,直线m为∠ABC的角平分线,l与m相交于P点.若∠BAC=60°,∠ACP=24°,则∠ABP是( )
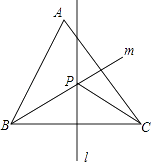
- A、 24°
- B、 30°
- C、 32°
- D、 36°
下列能判定三角形是等腰三角形的是( )
- A、 有两个角为30°、60°
- B、 有两个角为40°、80°
- C、 有两个角为50°、80°
- D、 有两个角为100°、120°
已知△ABC≌△A′B′C′,∠A=80°,∠B=40°,那么∠C′的度数为( )
- A、 80°
- B、 40°
- C、 60°
- D、 120°
△ABC中,∠A=∠B+∠C,则对△ABC的形状判断正确的是( )
- A、 锐角三角形
- B、 直角三角形
- C、 钝角三角形
- D、 等边三角形
如图是一副三角尺叠放的示意图,则∠α的度数为( )

- A、 75°
- B、 45°
- C、 30°
- D、 15°
一副三角板如图叠放在一起,则图中∠α的度数为( )
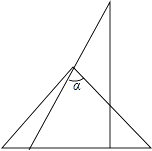
- A、 75°
- B、 60°
- C、 65°
- D、 55°
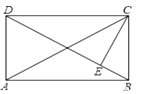
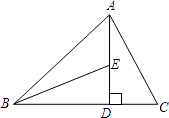
如图,点D、E分别是边AB、AC的中点,将△ADE沿着DE对折,点A落在BC边上的点F,若∠B=50°,则∠BDF的度数为( )
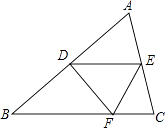
- A、 50°
- B、 70°
- C、 75°
- D、 80°
如图,在Rt△ABC中,∠ACB=90°,∠ABC=30°,将△ABC绕点C顺时针旋转 角(0°<
<180°)至△A′B′C, 使得点A′恰好落在AB边上,则
等于( ).
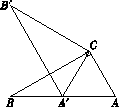
- A、 150°
- B、 90°
- C、 60°
- D、 30°
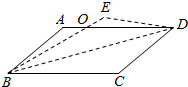
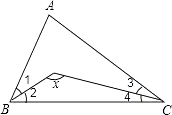
如图,△ABC中,∠B=∠C=∠EDF=α,BD=CF,BE=CD,则下列结论正确的是( )

- A、 2α+∠A=180°
- B、 α+∠A=90°
- C、 2α+∠A=90°
- D、 α+∠A=180°