单选题
- A、 0.4
- B、 2.5
- C、 4
- D、
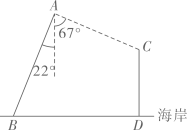
中国首次火星探测任务天问一号探测器在2021年2月10日成功被火星捕获,成为中国第一颗人造火星卫星,并在距离火星约11000米处,拍摄了火星全景图象.将11000用科学记数法表示应为( )
- A、
- B、
- C、
- D、
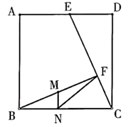
如图,  的度数为( )
的度数为( )
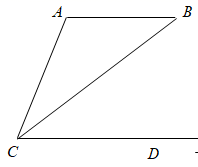
- A、
- B、
- C、
- D、
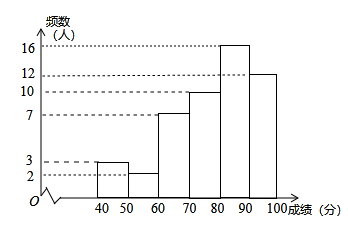
下列采用的调查方式中,不合适的是( )
- A、 了解洛河水的水质,采用抽样调查
- B、 了解洛阳市中学生睡眠时间,采用抽样调查
- C、 了解一批灯泡的使用寿命,采用全面调查
- D、 了解某个班级学生的数学成绩,采用全面调查
若点  ,
,  ,
,  在反比例函数
在反比例函数  的图象上,则
的图象上,则  ,
,  ,
,  的大小关系是( )
的大小关系是( )
- A、
- B、
- C、
- D、
定义  ,例如
,例如  ,若方程
,若方程  的一个根是
的一个根是  ,则此方程的另一个根是( )
,则此方程的另一个根是( )
- A、 -2
- B、 -3
- C、 -4
- D、 -5