单选题
如图所示,以BC为边的三角形共有( )

- A、 1个
- B、 2个
- C、 3个
- D、 4个
下列运算结果为a6的是( )
- A、 a3•a2
- B、 a9﹣a3
- C、 (a2)3
- D、 a18÷a3
对于任意的实数  ,总有意义的分式是( )
,总有意义的分式是( )
- A、
- B、
- C、
- D、
如图,AB=AC,点D,E分别在AB,AC上,补充下列一个条件后,不能判断△ABE ≌△ACD的是( )

- A、 ∠B=∠C
- B、 AD=AE
- C、 ∠BDC=∠CEB
- D、 BE=CD
芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一.它作为食品和药物,得到广泛的使用.经测算,一粒芝麻的质量约为  kg,将100粒芝麻的质量用科学记数法表示约为( )
kg,将100粒芝麻的质量用科学记数法表示约为( )
- A、
kg
- B、
kg
- C、
kg
- D、
kg
有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示.右边场地为长方形,长为  ,则宽为( )
,则宽为( )

- A、
- B、 1
- C、
- D、 a+b
已知△ABC, 两个完全一样的三角板如图摆放,它们的一组对应直角边分别在AB,AC上,且这组对应边所对的顶点重合于点M, 点M一定在( )
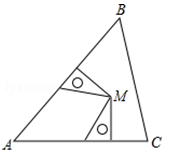
- A、 ∠A的平分线上
- B、AC边的高上
- C、BC边的垂直平分线上
- D、AB边的中线上
下列各式中,运算正确的是( )
- A、
- B、
- C、
- D、
如图,在△ABC中,AB=3,AC=4,BC=5,EF是BC的垂直平分线,P是直线EF上的任意一点,则PA+PB的最小值是( )

- A、 3
- B、 4
- C、 5
- D、 6
在下列因式分解的过程中,分解因式正确的是( )
- A、
- B、
- C、
- D、
如图,经过直线AB外一点C作这条直线的垂线,作法如下:
⑴任意取一点K,使点K和点C在AB的两旁.
⑵以点C为圆心,CK长为半径作弧,交AB于点D和E.
⑶分别以点D和点E为圆心,大于 的长为半径作弧,两弧相交于点F.
⑷作直线CF.
则直线CF就是所求作的垂线.根据以上尺规作图过程,若将这些点作为三角形的顶点,其中不一定是等腰三角形的为( )

- A、 △CDF
- B、 △CDK
- C、 △CDE
- D、 △DEF
若分式  的值为正数,则x需满足的条件是( )
的值为正数,则x需满足的条件是( )
- A、 x为任意实数
- B、
- C、
- D、
如图,在  中,
中,  ,过点
,过点  作
作  交
交  于点
于点  .若
.若  ,则
,则  的度数为( )
的度数为( )

- A、 18°
- B、 20°
- C、 30°
- D、 36°
如图,已知∠MON及其边上一点A, 以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C, 再以点C为圆心,AC长为半径画弧,恰好经过点B, 错误的结论是( ).
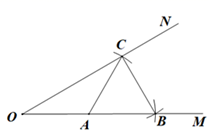
- A、
- B、 ∠OCB=90°
- C、 ∠MON=30°
- D、OC=2BC
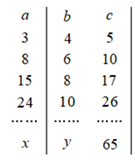
如果正整数a、b、c满足等式  ,那么正整数a、b、c叫做勾股数.某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )
,那么正整数a、b、c叫做勾股数.某同学将自己探究勾股数的过程列成下表,观察表中每列数的规律,可知x+y的值为( )
- A、 47
- B、 62
- C、 79
- D、 98




