单选题
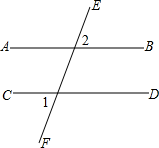
下列图形中，由 
，能得到 
的是（ ）
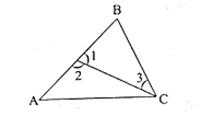
- A、
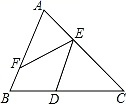
- B、
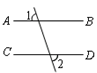
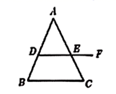
- C、
- D、
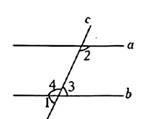
如图，直线a、b被直线c、d所截，下列条件能判定直线a∥b的是（ ）
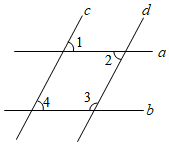
- A、 ∠1＝∠2
- B、 ∠1＝∠4
- C、 ∠2＝∠4
- D、 ∠3+∠4＝180°
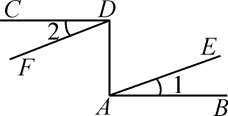
如图，要得到a∥b，则需要条件（ ）
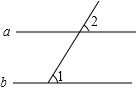
- A、 ∠1+∠2＝180°
- B、 ∠1＝∠2
- C、 ∠1+∠2＝90°
- D、 ∠1+∠2＝120°
如图，直线a，b被直线c所截，下列条件能判断a∥b的是（ ）
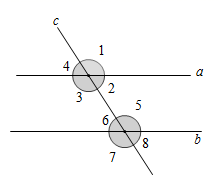
- A、 ∠3＝∠5
- B、 ∠4＝∠7
- C、 ∠2＋∠3＝180°
- D、 ∠1＝∠3
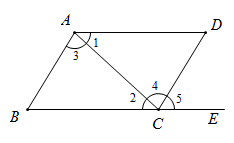
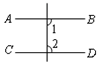
如图，在四边形ABCD中，连接BD，下列判断正确的是（ ）
- A、 若∠1=∠2，则AB//CD
- B、 若∠3=∠4，则AD//BC
- C、 若∠A+∠ABC=180°，则AB//CD
- D、 若∠A=∠C，∠ABC=∠ADC，则AB//CD
