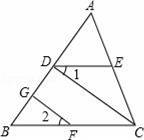
单选题
如图,已知l1∥l2 , l3分别与l1、l2相交,点A、B分别为l3 , l2上一点,且AB⊥l2 , 若∠1=52°,则∠2的度数为( )

- A、 28°
- B、 42°
- C、 38°
- D、 32°
如图,已知AB∥CD,则∠α、∠β和∠γ之间的关系为 ( )

- A、 β+γ-α=180°
- B、 α+γ=β
- C、 α+β+γ=360°
- D、 α+β-2γ=180°
已知:如图AB∥CD,EF交AB于G,交CD于F,FH平分∠EFD,交AB于H,∠AGE=50°,则∠BHF的度数为( )

- A、 115°
- B、 65°
- C、 50°
- D、 130°
如图,由 , 可以得到( )
, 可以得到( )

- A、
- B、
- C、
- D、
如图,AB∥CD,BC为∠ACD的角平分线,∠1=155°,则∠2为( )

- A、 155°
- B、 130°
- C、 150°
- D、 135°
如图,将一副三角尺按如图所示的位置在同一平面内摆放,其中∠ACB=∠CED=90°,∠B=30°,∠ECD=45°.若  ,CB与DE相交于点F , 则∠BCD的度数为( )
,CB与DE相交于点F , 则∠BCD的度数为( )

- A、 15°
- B、 20°
- C、 25°
- D、 30°
如图,直线AB∥CD , 点F是CD上一点,∠EFG=90°,EF交AB于M , 若∠CFG=35°,则∠AME的大小为( )

- A、 35°
- B、 55°
- C、 125°
- D、 130°
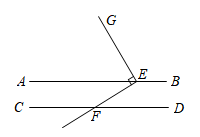
如图,  .点E在直线
.点E在直线  上,点F在直线
上,点F在直线  上,过点E作
上,过点E作  于E,如果
于E,如果  ,那么
,那么  的大小为( )
的大小为( )
- A、
- B、
- C、
- D、
如图,下列推理及所注明的理由都正确的是( )

- A、 因为
, 所以
(同位角相等,两直线平行)
- B、 因为
, 所以
(两直线平行,内错角相等)
- C、 因为
, 所以
(两直线平行,内错角相等)
- D、 因为
, 所以
(内错角相等,两直线平行)