单选题
下列各式从左到右的变形,是因式分解的是( )
- A、 ab+bc+d=a(b+c)+d
- B、 (a+2)(a-2)=a2-4
- C、 a3-1=(a-1)(a2+a+1)
- D、 6ab2=2ab•3b
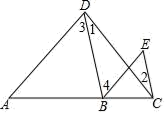
如图,不能判定AB∥CD的条件是( )
- A、 ∠1=∠2
- B、 ∠B+∠BCD=180°
- C、 ∠3=∠4
- D、 ∠B=∠5
已知a=(-0.3)0 , b=-3-1 , c= ,比较a,b,c的大小( )
,比较a,b,c的大小( )
- A、 a<b<c
- B、 b<c<a
- C、 a<c<b
- D、 b<a<c
若M=(x-2)(x-7),N=(x-6)(x-3),则M与N的关系为( )
- A、 M=N
- B、 M>N
- C、 M<N
- D、 M与N的大小由x的取值而定
(-8)2022+(-8)2021能被下列数整除的是( )
- A、 3
- B、 5
- C、 7
- D、 9
有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C,在△ABC中,∠DBA+∠DCA=40°,则∠A的度数是( )
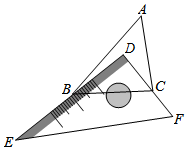
- A、 40°
- B、 45°
- C、 50°
- D、 55°
如图,正方形卡片A类,B类和长方形卡片C类若干张,要拼一个长为(a+mb),宽为(3a+b)的大长方形(m为常数),若知道需用到的B类卡片比A类卡片少1张,则共需C类卡片( )张.
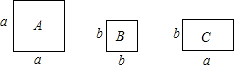
- A、 5
- B、 6
- C、 7
- D、 8
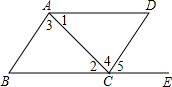
将△ABC纸片沿DE按如图的方式折叠.若∠C=50°,∠1=85°,则∠2的度数等于( )
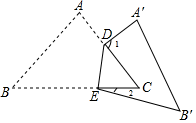
- A、 10°
- B、 15°
- C、 20°
- D、 25°