单选题
2022北京冬奥会吉祥物冰墩墩成了网红.通过平移左图吉祥物冰墩墩可以得到的图形是( )

- A、

- B、

- C、

- D、

以下调查中,适宜全面调查的是( )
- A、 了解中学生对神舟十四号发射现场直播的观看情况
- B、 了解淮南市民对八公山旅游景点的印象
- C、 了解一批新型节能灯的使用寿命
- D、 了解某航班上的乘客是否都持有“绿色健康码”
在下列实数中,无理数是( )
- A、
- B、 3.14
- C、
- D、
在平面直角坐标系中,点  在( )
在( )
- A、 第一象限
- B、 第二象限
- C、 第三象限
- D、 第四象限
已知关于x,y的方程组 的解是
的解是 , 则
, 则 的值是( )
的值是( )
- A、 2
- B、 1
- C、 1
- D、 0
将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )

- A、 60°
- B、 65°
- C、 75°
- D、 85°
如图, ,
,  ,
,  平分
平分 , 则
, 则 的度数等于( )
的度数等于( )

- A、 45°
- B、 52°
- C、 54°
- D、 60°
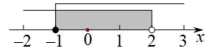
不等式组 的解集在数轴上表示为( )
的解集在数轴上表示为( )
- A、
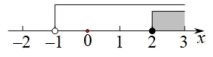
- B、

- C、
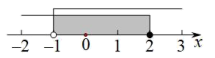
- D、