单选题
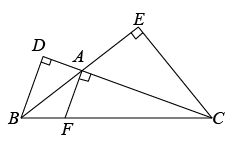
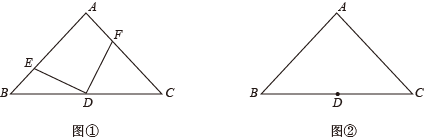
如图,是工人师傅用同一种材料制成的金属框架,已知 ,
,  ,
,  , 其中
, 其中 的周长为24cm,
的周长为24cm, , 则制成整个金属框架所需这种材料的总长度为( )
, 则制成整个金属框架所需这种材料的总长度为( )

- A、 45cm
- B、 48cm
- C、 51cm
- D、 54cm
下列条件中,能判定△ABC≌△DEF的是( )
- A、 AB=DE,BC=EF,∠A=∠D
- B、 ∠A=∠D,∠C=∠F,AC=EF
- C、 ∠B=∠E,∠A=∠D,AC=EF
- D、 ∠B=∠E,∠A=∠D,AB=DE
如图①是一张画有小方格的等腰直角三角形纸片,将图①按箭头方向折叠成图②,再将图②按箭头方向折叠成图③,再沿直线l剪掉直线l上方的三角形部分,最后把剩余部分展开,所得到的图形是( ).

- A、

- B、

- C、

- D、

下列图形:①两个正方形;②底边相等的两个等腰三角形;③每边都是2cm的两个三角形;④半径都是1.5cm的两个圆.其中是一对全等图形的有( )
- A、 1个
- B、 2个
- C、 3个
- D、 4个
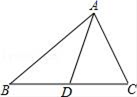
等腰三角形的一个角是50°,则一腰上的高与底边的夹角是( )
- A、 25°
- B、 40°
- C、 25°或40°
- D、 25°或60°
下面是“求作∠AOB的角平分线”的尺规作图过程( )
已知:钝角∠AOB.
求作:∠AOB的角平分线.
作法:
①在OA和OB上,分别截取OD,OE,使OD=OE;
②分别以D,E为圆心,大于DE的长为半径作弧,交∠AOB内部的点C;
③作射线OC.
所以,射线OC就是所求作的∠AOB的角平分线.

上述尺规作图的依据是( )
- A、 ASA
- B、 SAS
- C、 AAS
- D、 SSS
折纸是我国的传统文化,折纸不仅和自然科学结合在一起,还发展出了折纸几何学,成为现代几何学的一个分支.如图,将一长方形纸条首先沿EF进行第一次折叠,使得C,D两点落在 ,
,  的位置,再将纸条沿GF折叠(GF与BC在同一直线上),使得
的位置,再将纸条沿GF折叠(GF与BC在同一直线上),使得 ,
,  分别落在
分别落在 ,
,  的位置.若3∠ EFB=∠EF
的位置.若3∠ EFB=∠EF , 则∠GEF的度数为( )
, 则∠GEF的度数为( )

- A、 30°
- B、 36°
- C、 45°
- D、 60°
如图为5×5的方格,点A,B,C均在格点上,点P在方格的其它格点上,且点A,B,C,P构成一个轴对称的点阵图,则符合条件的P点的位置有( )

- A、 5个
- B、 4个
- C、 3个
- D、 2个
如图,ABCD是一张长方形纸片,将AD,BC折起,使A、B两点重合于CD边上的P点,然后压平得折痕EF与GH.若PE=8cm,PG=6cm,EG=10cm,则长方形纸片ABCD的面积为( )
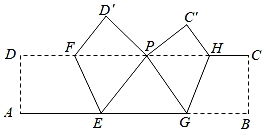
- A、 105.6cm2
- B、 110.4cm2
- C、 115.2cm2
- D、 124.8cm2